Deep Neural Networks Final Model parameters

Training neural network requires specifying an initial value of the weights. You'll see that a well-chosen initialization method could improve learning and accuracy

PyLessons
Published May 07, 2019

Improving Deep Neural Networks - Initialization:

Training neural network requires specifying an initial value of the weights. A well-chosen initialization method would improve learning and accuracy.

If you were reading my previous tutorial pars, you probably followed my instructions for weight initialization, and it has worked out so far. But how do we choose the initialization for another neural network? In this part, I will show you that different initialization methods can lead to different results.

A well-chosen initialization can speed up the convergence of gradient descent and increase the odds of gradient descent converging to a lower training error.

I will use code from my last tutorial, where we used to classify circles. Before we used random weights initialization, now we'll try "He Initialization", this is named for the first author of He et al., 2015. (If you have heard of "Xavier initialization", this is similar, except Xavier initialization uses a scaling factor for the weights W[l] of:

1layer_dims[l-1], where He initialization would use 2layer_dims[l-1]

Before, we used the following code:

def initialize_parameters_deep(layer_dimension):
    parameters = {}

    L = len(layer_dimension)

    for l in range(1, L):
        parameters["W" + str(l)] = np.random.randn(layer_dimension[l], layer_dimension[l-1]) * 0.01
        parameters["b" + str(l)] = np.zeros((layer_dimension[l], 1))

    return parameters

The only difference is that instead of multiplying np.random.randn(..,..) by 0.01, we will multiply it by sqrt(2/dimensions of the previous layer), which is what "He" initialization recommends for layers with a ReLU activation:

def initialize_parameters_he(layer_dimension):
    parameters = {}

    L = len(layer_dimension)

    for l in range(1, L):
        parameters["W" + str(l)] = np.random.randn(layer_dimension[l], layer_dimension[l-1]) * np.sqrt(2./layers_dims[l-1])
        parameters["b" + str(l)] = np.zeros((layer_dimension[l], 1))

    return parameters

At first, let's test our results with the random initialization, that we could compare the difference:

Cost after iteration 14600: 0.495909
Cost after iteration 14700: 0.496088
Cost after iteration 14800: 0.496531
Cost after iteration 14900: 0.496314
train accuracy: 72.33333333333333 %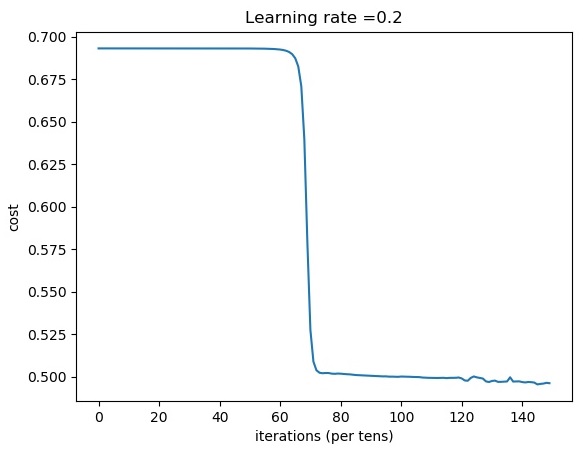
 

From this above plot, we can see that cost drops only after 8000 training steps.

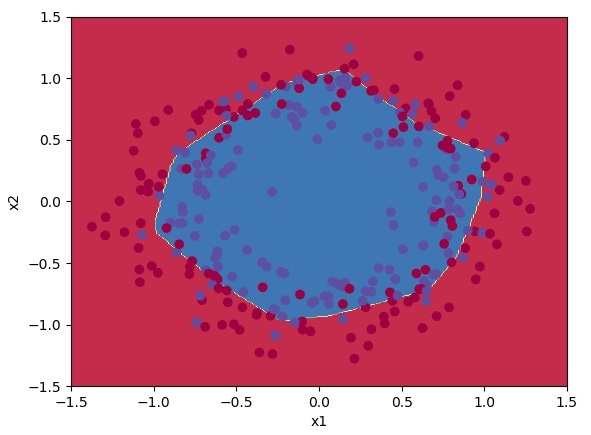
Classification results are quite fine for us.

Cost after iteration 14600: 0.456906
Cost after iteration 14700: 0.457210
Cost after iteration 14800: 0.463999
Cost after iteration 14900: 0.467439
train accuracy: 73.66666666666667 %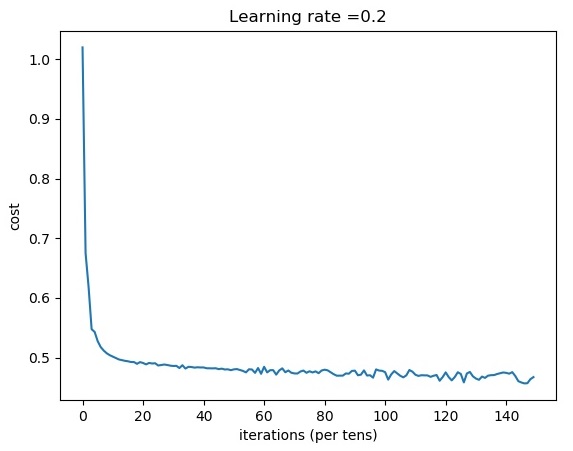

From this above plot, we can see that cost drops almost instantly; we don't need to wait for 8000 steps to see improvement.

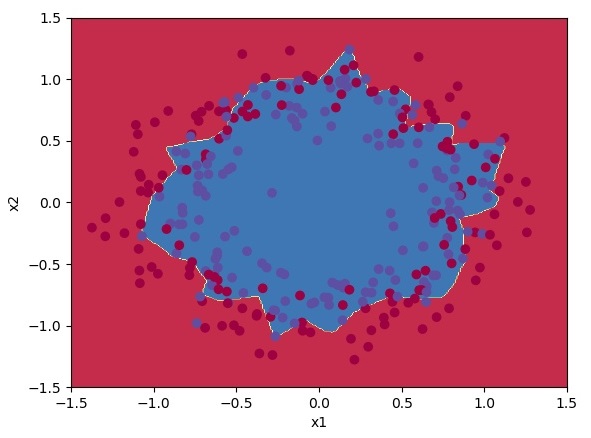
Classification results are 1% better than using random initialization.

Conclusion:

We should remember that different parameters initialization methods lead to different results. Random initialization is used to break symmetry and to make sure different hidden units can learn different things.

Don't initialize to values that are too large, but initializing with overly large random numbers you'll slow down the optimization. As you can see, "He" initialization works well for networks with ReLU activations.

This is the last deep learning tutorial. To get better results, you can optimize this deep neural network by implementing L2 regularization, dropout, and gradient checking. You can try to optimize using momentum, adam optimizer or implement training with mini-batches.

Full tutorial code and cats vs. dogs image data-set can be found on my GitHub page.

Home