Deep Neural Networks forward propagation

Now when we have initialized our parameters, we will do the forward propagation module. We will start by implementing some basic functions that we will use later when implementing the model. We will complete three functions in this order:

• LINEAR;
• LINEAR -> ACTIVATION where ACTIVATION will be either ReLU or Sigmoid;
• [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID (whole model).

I could write all these functions in one block, but then it's harder to understand code to leave it for learning purposes. I'll remind you that the linear forward module (vectorized over all the examples) computes the following equation:

$Z^{\left[l\right]}=W^{\left[l\right]}{A}^{[l-1]}+b^{\left[l\right]}$

where A[0]=X

Code for our linear_forward function:

Arguments:

A - activations from previous layer (or input data): (size of the previous layer, number of examples);
W - weights matrix: NumPy array of shape (size of current layer, size of the previous layer);
b - bias vector, NumPy array of shape (size of the current layer, 1).

Return:

Z - the input of the activation function, also called a pre-activation parameter;
cache - a python dictionary containing "A", "W", and "b"; stored for computing the backward pass efficiently.

def linear_forward(A, W, b):

    Z = np.dot(W,A)+b

    cache = (A, W, b)
    
    return Z, cache

Linear-Activation Forward function:

In this tutorial, we will test two activation functions, Sigmoid and ReLu:

Sigmoid: 

$\sigma \left(Z\right)=\sigma (WA+b)=\frac{1}{1+e^{-(WA+b)}}$

I will write you the sigmoid function. This function returns two items: the activation value "a" and a "cache" that contains "Z" (it's what we will feed into the corresponding backward function). To use it, we'll call:

A, activation_cache = sigmoid(Z)

Sigmoid function:

def sigmoid(Z):
    """
    Numpy sigmoid activation implementation
    Arguments:
    Z - numpy array of any shape
    Returns:
    A - output of sigmoid(z), same shape as Z
    cache - returns Z as well, useful during backpropagation
    """
    A = 1/(1+np.exp(-Z))
    cache = Z
    return A, cache

ReLu: The mathematical formula for ReLu is A=RELU(Z)=max(0, Z). I will write you the ReLu function. This function returns two items: the activation value "A" and a "cache" that contains "Z" (it's what we will feed into the corresponding backward function). To use it, we'll call:

A, activation_cache = relu(Z)

ReLu function:

def relu(Z):
    """
    Numpy Relu activation implementation
    Arguments:
    Z - Output of the linear layer, of any shape
    Returns:
    A - Post-activation parameter, of the same shape as Z
    cache - a python dictionary containing "A"; stored for computing the backward pass efficiently
    """
    A = np.maximum(0,Z)  
    cache = Z 
    return A, cache

For more convenience, we are going to group two functions (Linear and Activation) into one function (LINEAR->ACTIVATION). Hence, we will implement a function that does the LINEAR forward step followed by an ACTIVATION forward step.

Code for our linear_activation_forward function:

Arguments:

A_prev - activations from previous layer (or input data): (size of the previous layer, number of examples);
W - weights matrix: NumPy array of shape (size of current layer, size of the previous layer);
b - bias vector, NumPy array of shape (size of the current layer, 1);
activation - the activation to be used in this layer, stored as a text string: "sigmoid" or "relu".

Return:

A - the output of the activation function, also called the post-activation value;
cache - a python dictionary containing "linear_cache" and "activation_cache" stored efficiently for computing the backward pass.

def linear_activation_forward(A_prev, W, b, activation):
    
    if activation == "sigmoid":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".       
        Z, linear_cache = linear_forward(A_prev,W,b)
        A, activation_cache = sigmoid(Z)      
    
    elif activation == "relu":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".      
        Z, linear_cache = linear_forward(A_prev,W,b)
        A, activation_cache = relu(Z)
        
    cache = (linear_cache, activation_cache)

    return A, cache

L-Layer Model implementation:

For more convenience when implementing the L-layer Neural Network, we will need a function that replicates the above (linear_activation_forward with RELU) L−1 times and then follows that with one linear_activation_forward SIGMOID.

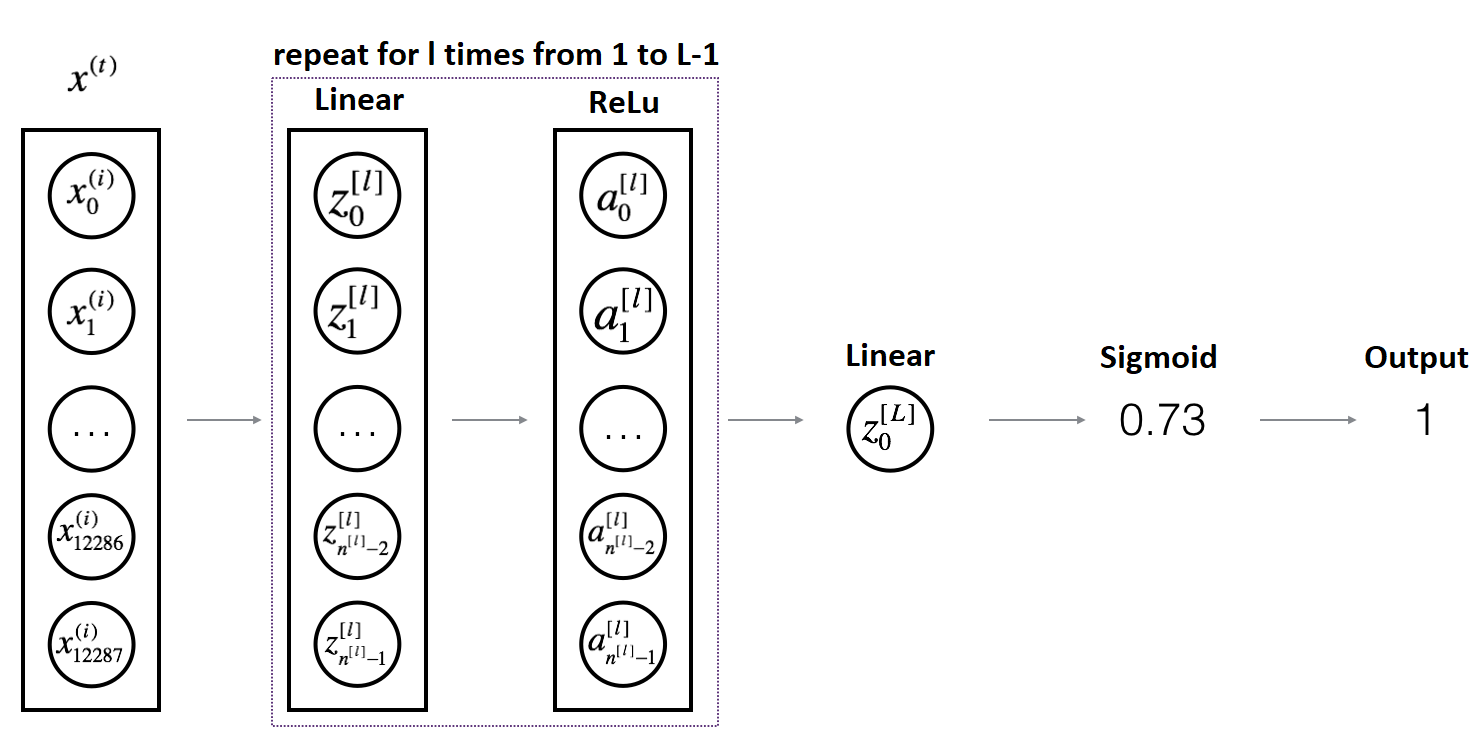
So writing our code, we'll use the functions we had previously written. In the code below, the variable AL will denote:

$$\begin{gathered} A^{\left[L\right]}=\sigma \left(Z^{\left[L\right]}\right)=\sigma (W^{\left[L\right]}{A}^{[L-1]}+b^{\left[L\right]}), \\ \text{This is sometimes is called }\mathbf{\text{Yhat}}\text{, i. e., this is }\hat{Y}\text{.} \end{gathered}$$

Code for our L_model_forward function:

Arguments:

X - data, numpy array of shape (input size, number of examples);
parameters - output of initialize_parameters_deep() function.

Return:

AL - last post-activation value;
caches - list of caches containing every cache of linear_activation_forward() (there are L-1 of them, indexed from 0 to L-1)

def L_model_forward(X, parameters):
    caches = []
    A = X

    # number of layers in the neural network
    L = len(parameters) // 2
    
    # Using a for loop to replicate [LINEAR->RELU] (L-1) times
    for l in range(1, L):
        A_prev = A 

        # Implementation of LINEAR -> RELU.
        A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], activation = "relu")

        # Adding "cache" to the "caches" list.
        caches.append(cache)

    
    # Implementation of LINEAR -> SIGMOID.
    AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], activation = "sigmoid")
    
    # Adding "cache" to the "caches" list.
    caches.append(cache)
            
    return AL, caches

Now we can test the functions we implemented in this tutorial with random numbers to see if they work well. I'll initialize the neural network with 2 deep layers, with 4 inputs and one output. For inputs, I'll use a command  np.random.randn(input size, number of examples). Then I'll call the L_model_forward function:

layers_dims = [4,3,2,1]
parameters = initialize_parameters_deep(layers_dims)
X = np.random.randn(4,10)
AL, caches = L_model_forward(X, parameters)

print("X.shape = ",X.shape)
print("AL =",AL)
print("Length of caches list =",len(caches))
print("parameters:",parameters)

I received such results; you may receive them a little different:

X.shape = (4, 10)
AL = [[0.5  0.5  0.5  0.5  0.50000402  0.5  0.50000157  0.5  0.5  0.50000136]]
Length of caches list = 3
parameters: {
       'W1': array([[ 0.00315373, -0.00545479,  0.00453286, -0.00320905],
       [-0.00219829, -0.00134337,  0.0017775 ,  0.01365787],
       [-0.01525445,  0.01085829, -0.00822895,  0.00067442]]), 
       'b1': array([[0.],
       [0.],
       [0.]]), 
       'W2': array([[ 0.00094041, -0.01439561, -0.0117556 ],
       [-0.00528372, -0.00807826,  0.02711167]]), 
       'b2': array([[0.],
       [0.]]), 
       'W3': array([[0.00180661, 0.01540206]]), 
       'b3': array([[0.]])}

Full tutorial code:

import numpy as np

def sigmoid(Z):
    """
    Numpy sigmoid activation implementation
    Arguments:
    Z - numpy array of any shape
    Returns:
    A - output of sigmoid(z), same shape as Z
    cache -- returns Z as well, useful during backpropagation
    """
    A = 1/(1+np.exp(-Z))
    cache = Z
    return A, cache

def relu(Z):
    """
    Numpy Relu activation implementation
    Arguments:
    Z - Output of the linear layer, of any shape
    Returns:
    A - Post-activation parameter, of the same shape as Z
    cache - a python dictionary containing "A"; stored for computing the backward pass efficiently
    """
    A = np.maximum(0,Z)  
    cache = Z 
    return A, cache

def initialize_parameters(input_layer, hidden_layer, output_layer):
    # initialize 1st layer output and input with random values
    W1 = np.random.randn(hidden_layer, input_layer) * 0.01
    # initialize 1st layer output bias
    b1 = np.zeros((hidden_layer, 1))
    # initialize 2nd layer output and input with random values
    W2 = np.random.randn(output_layer, hidden_layer) * 0.01
    # initialize 2nd layer output bias
    b2 = np.zeros((output_layer,1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

def initialize_parameters_deep(layer_dimension):
    parameters = {}

    L = len(layer_dimension)

    for l in range(1, L):
        parameters["W" + str(l)] = np.random.randn(layer_dimension[l], layer_dimension[l-1]) * 0.01
        parameters["b" + str(l)] = np.zeros((layer_dimension[l], 1))

    return parameters

def linear_forward(A, W, b):

    Z = np.dot(W,A)+b

    cache = (A, W, b)
    
    return Z, cache

def linear_activation_forward(A_prev, W, b, activation):
    
    if activation == "sigmoid":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".       
        Z, linear_cache = linear_forward(A_prev,W,b)
        A, activation_cache = sigmoid(Z)      
    
    elif activation == "relu":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".      
        Z, linear_cache = linear_forward(A_prev,W,b)
        A, activation_cache = relu(Z)
        
    cache = (linear_cache, activation_cache)

    return A, cache

def L_model_forward(X, parameters):
    caches = []
    A = X

    # number of layers in the neural network
    L = len(parameters) // 2
    
    # Using a for loop to replicate [LINEAR->RELU] (L-1) times
    for l in range(1, L):
        A_prev = A 

        # Implementation of LINEAR -> RELU.
        A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], activation = "relu")

        # Adding "cache" to the "caches" list.
        caches.append(cache)

    
    # Implementation of LINEAR -> SIGMOID.
    AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], activation = "sigmoid")
    
    # Adding "cache" to the "caches" list.
    caches.append(cache)
            
    return AL, caches

layer_dims = [4,3,2,2,1]
parameters = initialize_parameters_deep(layer_dims)
X = np.random.rand(4, 10)
AL, caches = L_model_forward(X, parameters)

print("X.shape =", X.shape)
print("AL =", AL)
print("Lenght of caches list = ", len(caches))
print("parameters:", parameters)