Deep Neural Networks backward propagation

Cost function:

So up to this point, we have initialized our deep parameters and wrote forward propagation module. Now we will implement the cost function and backward propagation module. Same as before, we need to compute the cost because we want to check if our model is actually learning.
To compute the cross-entropy cost J, we'll be using the formula we already saw before:

$-\frac{1}{m}\sum _{i=1}^m\left(y^{\left(i\right)}\log \left(a^{\left[L\right]\left(i\right)}\right)-(1-y^{\left(i\right)})\log (1-a^{\left[L\right]\left(i\right)})\right)$

Code for our compute_cost function:

Arguments:

AL - probability vector corresponding to your label predictions, shape (1, number of examples).
Y - true "label" vector (for example: containing 0 if a dog, 1 if a cat), shape (1, number of examples).

Return:

cost - cross-entropy cost.

def compute_cost(AL, Y):
    # number of examples
    m = Y.shape[1]

    # Compute loss from AL and y.
    cost = -1./m * np.sum(Y*np.log(AL)+(1-Y)*np.log(1-AL))

    # To make sure our cost's shape is what we expect (e.g. this turns [[23]] into 23).
    cost = np.squeeze(cost)
    
    return cost

This is only one line of code, so we won't test it, as it was tested in my previous tutorials.

Backward propagation function:

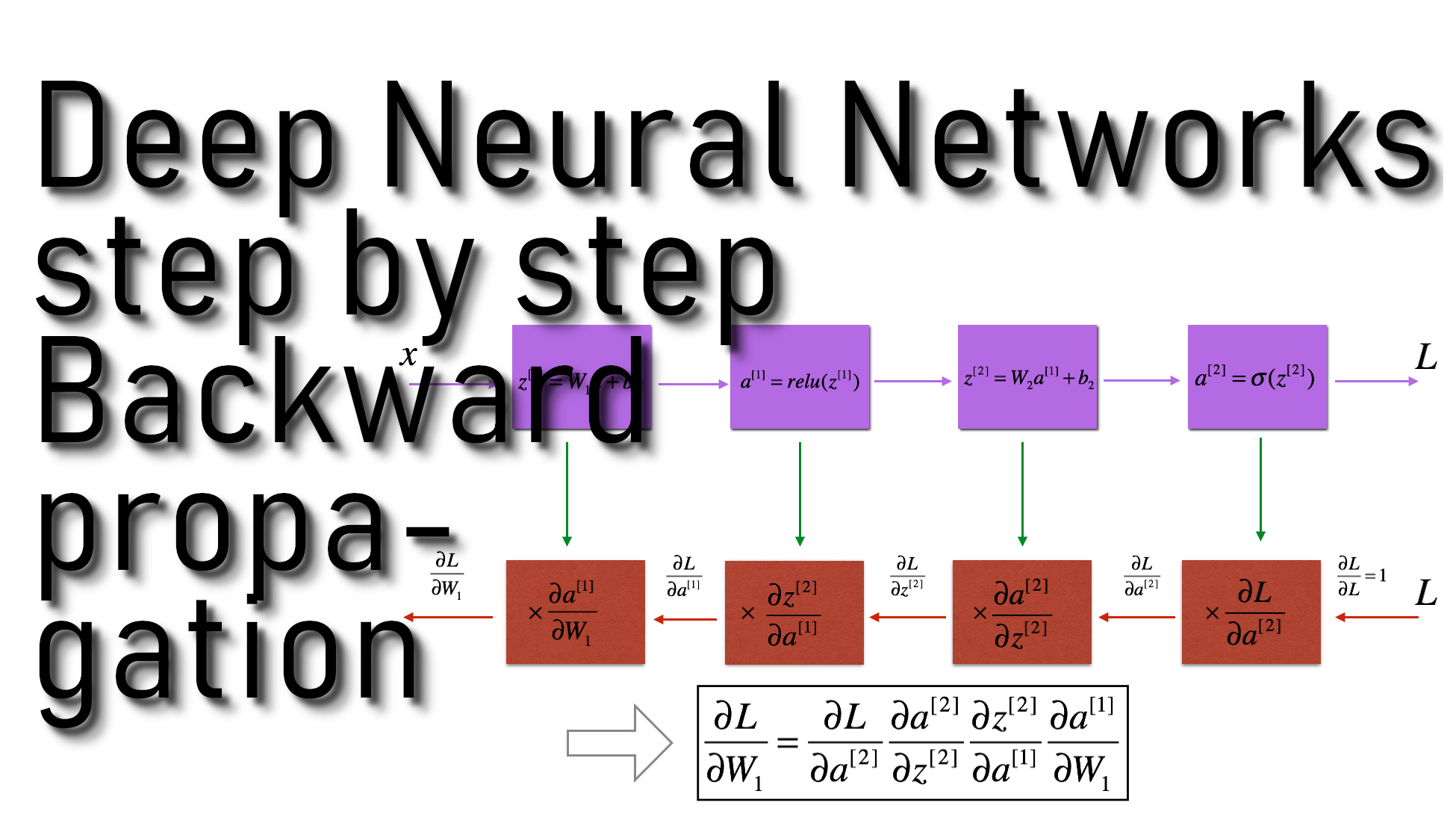
Just like with the forward propagation, we will implement helper functions for backpropagation. We know that propagation is used to calculate the gradient of the loss function for the parameters. We need to write Forward and Backward propagation for LINEAR->RELU->LINEAR->SIGMOID model. This will look like this:

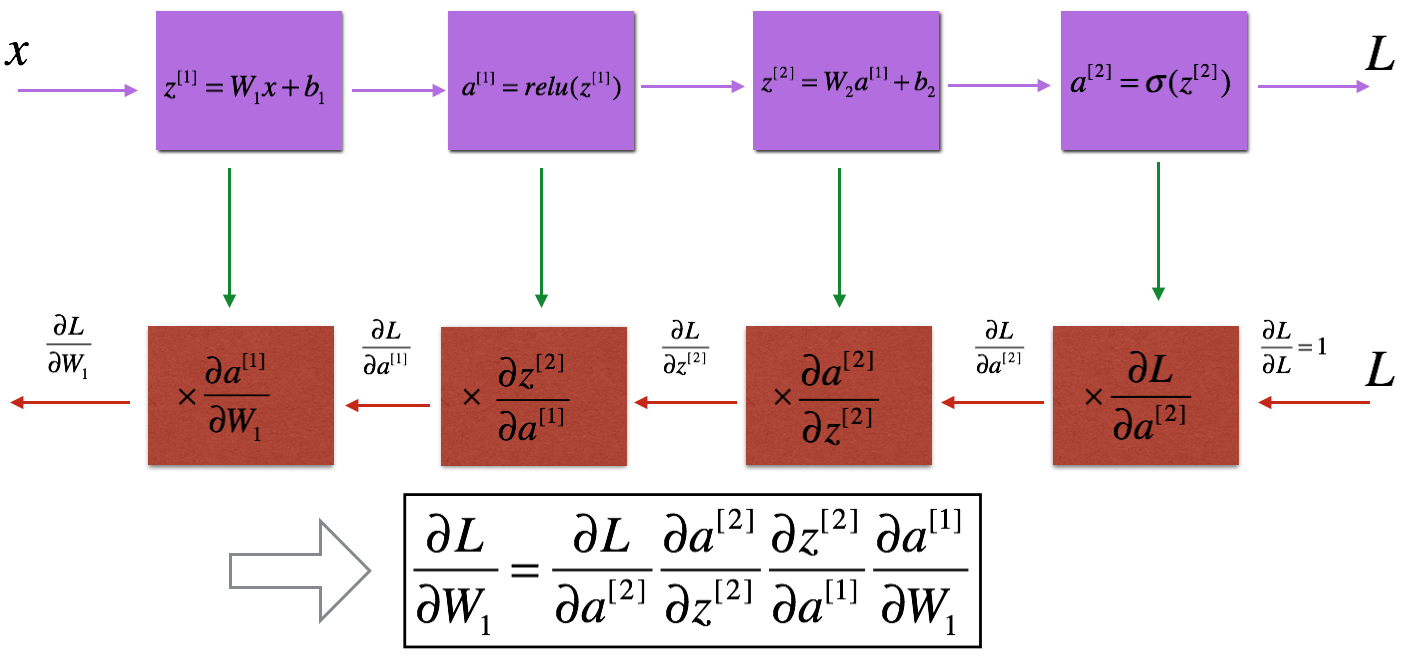
Similar to the forward propagation, we are going to build the backward propagation in three steps:

• LINEAR backward;
• LINEAR -> ACTIVATION backward where ACTIVATION computes the derivative of either the ReLU or sigmoid activation;
• [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID backward (whole model)

Linear backward:

For layer l, the linear part is:

$Z^{\left[l\right]}=W^{\left[l\right]}{A}^{[l-1]}+b^{\left[l\right]}$

I suppose we have already calculated the derivative:

$d{Z}^{\left[l\right]}=\frac{\partial L}{\partial Z^{\left[l\right]}} \text{and we want to get} (d{W}^{\left[l\right]}, d{A}^{[l-1]}, d{b}^{\left[l\right]})$

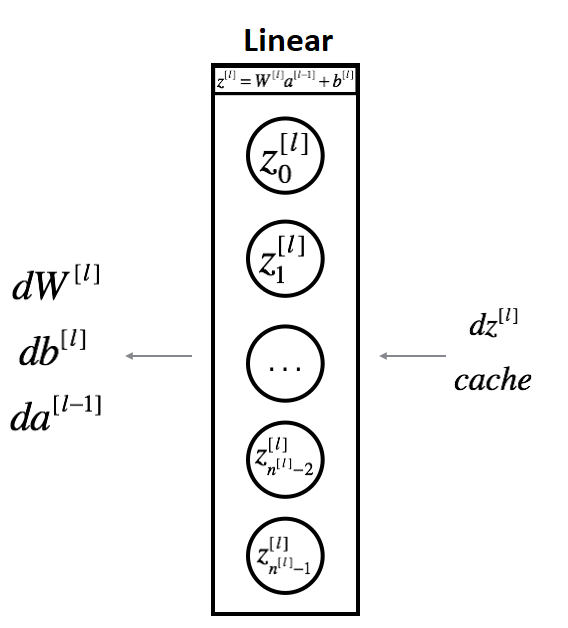
Three outputs (dW[l], db[l], dA[l]) will be computed using the input dZ[l]. Here are the formulas we need from our two-layer neural networks tutorial series:

$$\begin{gathered} d{W}^{\left[l\right]}=\frac{\partial L}{\partial b^{\left[l\right]}}=\frac{1}{m}d{Z}^{\left[l\right]}{A}^{[l-1]T} \\ d{b}^{\left[l\right]}=\frac{\partial L}{\partial b^{\left[l\right]}}=\frac{1}{m}\sum _{i=1}^{m}d{Z}^{\left[l\right]\left(i\right)} \\ d{A}^{[l-1]}=\frac{\partial L}{\partial A^{[l-1]}}=W^{\left[l\right]T}d{Z}^{\left[l\right]} \end{gathered}$$

Code for our linear_backward function:

Arguments:

dZ - Gradient of the cost concerning the linear output (of current layer l);
cache - tuple of values (A_prev, W, b) coming from the forward propagation in the current layer.

Return:

dA_prev - Gradient of the cost concerning the activation (of the previous layer l-1), the same shape as A_prev;
dW - Gradient of the cost to W (current layer l), the same shape as W;
db - Gradient of the cost to b (current layer l), the same shape as b.

def linear_backward(dZ, cache):
    A_prev, W, b = cache
    m = A_prev.shape[1]

    dW = 1./m * np.dot(dZ, A_prev.T)
    db = 1./m * np.sum(dZ, axis=1, keepdims=True)
    dA_prev = np.dot(W.T, dZ)
    
    return dA_prev, dW, db

Linear-Activation backward function:

Next, we will create a function that merges the two helper functions: linear_backward and the backward step for the activation linear_activation_backward.

To implement linear_activation_backward, we will write two backward functions:

• sigmoid_backward: the backward propagation for SIGMOID unit:

def sigmoid_backward(dA, cache):
    """
    The backward propagation for a single SIGMOID unit.
    Arguments:
    dA - post-activation gradient, of any shape
    cache - 'Z' where we store for computing backward propagation efficiently
    Returns:
    dZ - Gradient of the cost with respect to Z
    """
    Z = cache 
    s = 1/(1+np.exp(-Z))
    dZ = dA * s * (1-s)
    return dZ

• relu_backward: the backward propagation for RELU unit:

def relu_backward(dA, cache):
    """
    The backward propagation for a single RELU unit.
    Arguments:
    dA - post-activation gradient, of any shape
    cache - 'Z' where we store for computing backward propagation efficiently
    Returns:
    dZ - Gradient of the cost with respect to Z
    """
    Z = cache
    # just converting dz to a correct object.
    dZ = np.array(dA, copy=True)
    # When z <= 0, we should set dz to 0 as well. 
    dZ[Z <= 0] = 0
    return dZ

If g(.) is the activation function, sigmoid_backward and relu_backward compute:

$d{Z}^{\left[l\right]}=d{A}^{\left[l\right]}·g\text{'}\left(Z^{\left[l\right]}\right)$

Code for our linear_activation_backward function:

Arguments:

dA - post-activation gradient for current layer l;
cache - tuple of values (linear_cache, activation_cache) we store for computing backward propagation efficiently;
activation - the activation to be used in this layer, stored as a text string: "sigmoid" or "relu".

Return:

dA_prev - Gradient of the cost to the activation (of the previous layer l-1), the same shape as A_prev;
dW - Gradient of the cost to W (current layer l), the same shape as W;
db - Gradient of the cost to b (current layer l), the same shape as b.

def linear_activation_backward(dA, cache, activation):

    linear_cache, activation_cache = cache
    
    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
        
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    
    return dA_prev, dW, db

Full tutorial code:

import numpy as np

def sigmoid(Z):
    """
    Numpy sigmoid activation implementation
    Arguments:
    Z - numpy array of any shape
    Returns:
    A - output of sigmoid(z), same shape as Z
    cache -- returns Z as well, useful during backpropagation
    """
    A = 1/(1+np.exp(-Z))
    cache = Z
    return A, cache

def relu(Z):
    """
    Numpy Relu activation implementation
    Arguments:
    Z - Output of the linear layer, of any shape
    Returns:
    A - Post-activation parameter, of the same shape as Z
    cache - a python dictionary containing "A"; stored for computing the backward pass efficiently
    """
    A = np.maximum(0,Z)  
    cache = Z 
    return A, cache

def sigmoid_backward(dA, cache):
    """
    The backward propagation for a single SIGMOID unit.
    Arguments:
    dA - post-activation gradient, of any shape
    cache - 'Z' where we store for computing backward propagation efficiently
    Returns:
    dZ - Gradient of the cost with respect to Z
    """
    Z = cache 
    s = 1/(1+np.exp(-Z))
    dZ = dA * s * (1-s)
    return dZ

def relu_backward(dA, cache):
    """
    The backward propagation for a single RELU unit.
    Arguments:
    dA - post-activation gradient, of any shape
    cache - 'Z' where we store for computing backward propagation efficiently
    Returns:
    dZ - Gradient of the cost with respect to Z
    """
    Z = cache
    dZ = np.array(dA, copy=True) # just converting dz to a correct object.
    # When z <= 0, you should set dz to 0 as well. 
    dZ[Z <= 0] = 0
    return dZ

def initialize_parameters(input_layer, hidden_layer, output_layer):
    # initialize 1st layer output and input with random values
    W1 = np.random.randn(hidden_layer, input_layer) * 0.01
    # initialize 1st layer output bias
    b1 = np.zeros((hidden_layer, 1))
    # initialize 2nd layer output and input with random values
    W2 = np.random.randn(output_layer, hidden_layer) * 0.01
    # initialize 2nd layer output bias
    b2 = np.zeros((output_layer,1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

def initialize_parameters_deep(layer_dimension):
    parameters = {}

    L = len(layer_dimension)

    for l in range(1, L):
        parameters["W" + str(l)] = np.random.randn(layer_dimension[l], layer_dimension[l-1]) * 0.01
        parameters["b" + str(l)] = np.zeros((layer_dimension[l], 1))

    return parameters

def linear_forward(A, W, b):

    Z = np.dot(W,A)+b

    cache = (A, W, b)
    
    return Z, cache

def linear_activation_forward(A_prev, W, b, activation):
    
    if activation == "sigmoid":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".       
        Z, linear_cache = linear_forward(A_prev,W,b)
        A, activation_cache = sigmoid(Z)      
    
    elif activation == "relu":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".      
        Z, linear_cache = linear_forward(A_prev,W,b)
        A, activation_cache = relu(Z)
        
    cache = (linear_cache, activation_cache)

    return A, cache

def L_model_forward(X, parameters):
    caches = []
    A = X

    # number of layers in the neural network
    L = len(parameters) // 2
    
    # Using a for loop to replicate [LINEAR->RELU] (L-1) times
    for l in range(1, L):
        A_prev = A 

        # Implementation of LINEAR -> RELU.
        A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], activation = "relu")

        # Adding "cache" to the "caches" list.
        caches.append(cache)

    
    # Implementation of LINEAR -> SIGMOID.
    AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], activation = "sigmoid")
    
    # Adding "cache" to the "caches" list.
    caches.append(cache)
            
    return AL, caches

def compute_cost(AL, Y):
    # number of examples
    m = Y.shape[1]

    # Compute loss from AL and y.
    cost = -np.sum(Y*np.log(AL)+(1-Y)*np.log(1-AL))/m

    # To make sure our cost's shape is what we expect (e.g. this turns [[23]] into 23).
    cost = np.squeeze(cost)
    
    return cost

def linear_backward(dZ, cache):
    A_prev, W, b = cache
    m = A_prev.shape[1]

    dW = 1./m * np.dot(dZ, A_prev.T)
    db = 1./m * np.sum(dZ, axis=1, keepdims=True)
    dA_prev = np.dot(W.T, dZ)
    
    return dA_prev, dW, db

def linear_activation_backward(dA, cache, activation):

    linear_cache, activation_cache = cache
    
    if activation == "relu":
        dZ = relu_backward(dA, cache[1])
        dA_prev, dW, db = linear_backward(dZ, cache[0])
   
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, cache[1])
        dA_prev, dW, db = linear_backward(dZ, cache[0])
    
    return dA_prev, dW, db


layer_dims = [4,3,2,2,1]
parameters = initialize_parameters_deep(layer_dims)
X = np.random.rand(4, 4)
Y = np.array([[1, 1, 0, 0]])
AL, caches = L_model_forward(X, parameters)

print("X.shape =", X.shape)
print("AL =", AL)
print("Lenght of caches list = ", len(caches))
print("parameters:", parameters)
print("cost = ", compute_cost(AL, Y))