Best choice of learning rate in Logistic Regression

For Gradient Descent to work, we must choose the learning rate wisely. The learning rate α determines how rapidly we update the parameters. If the learning rate is too large, we may "overshoot" the optimal value. Similarly, if it is too small, we will need too many iterations to converge to the best values. That's why it is crucial to use a well-tuned learning rate.

So we'll compare the learning curve of our model with several choices of learning rates. Run the code below. Feel free also to try different values than I have initialized.
GitHub link to full code.

learning_rates = [0.001, 0.003, 0.005, 0.01]
models = {}
for i in learning_rates:
    print ("learning rate is: ",i)
    models[i] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 500, learning_rate = i, print_cost = False)
    print ("-------------------------------------------------------")

for i in learning_rates:
    plt.plot(np.squeeze(models[i]["costs"]), label= str(models[i]["learning_rate"]))

plt.ylabel('cost')
plt.xlabel('iterations (hundreds)')

legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()

We'll receive such training and testing accuracy with different learning rates:

the learning rate is: 0.001
train accuracy: 63.628790403198934 %
test accuracy: 59.0 %
---------------------------------------------------------
learning rate is: 0.002
train accuracy: 66.27790736421193 %
test accuracy: 60.0 %
---------------------------------------------------------
learning rate is: 0.003
train accuracy: 68.24391869376875 %
test accuracy: 58.6 %
---------------------------------------------------------
learning rate is: 0.005
train accuracy: 54.08197267577474 %
test accuracy: 53.0 %
---------------------------------------------------------
learning rate is: 0.01
train accuracy: 54.18193935354882 %
test accuracy: 53.3 %
---------------------------------------------------------

Results of learning rates can be seen in the graph below:

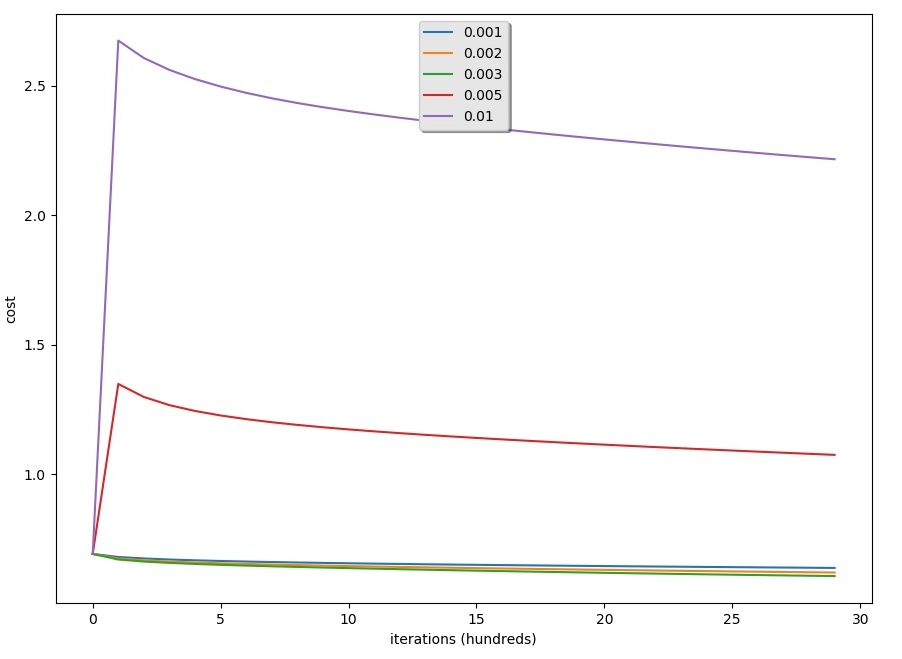
Results:

• Different learning rates give different costs and different predictions results;
• If the learning rate is too large (0.01), the cost may oscillate up and down. Using 0.01 still eventually ends up at a good value for the cost.
• A lower-cost doesn't mean a better model. You have to check if there is possibly over-fitting. It happens when the training accuracy is a lot higher than the test accuracy;
• In deep learning, it's usually recommended to choose the learning rate that minimizes the cost function.

What to remember from this Logistic Regression tutorial series:

1. Preprocessing the dataset is important;
2. It's better to implement each function separately: initialize(), propagate(), optimize(). Then built a final model();
3. Tuning the learning rate ("hyperparameter") can make a big difference to the algorithm. We will see more examples of this in future tutorials.