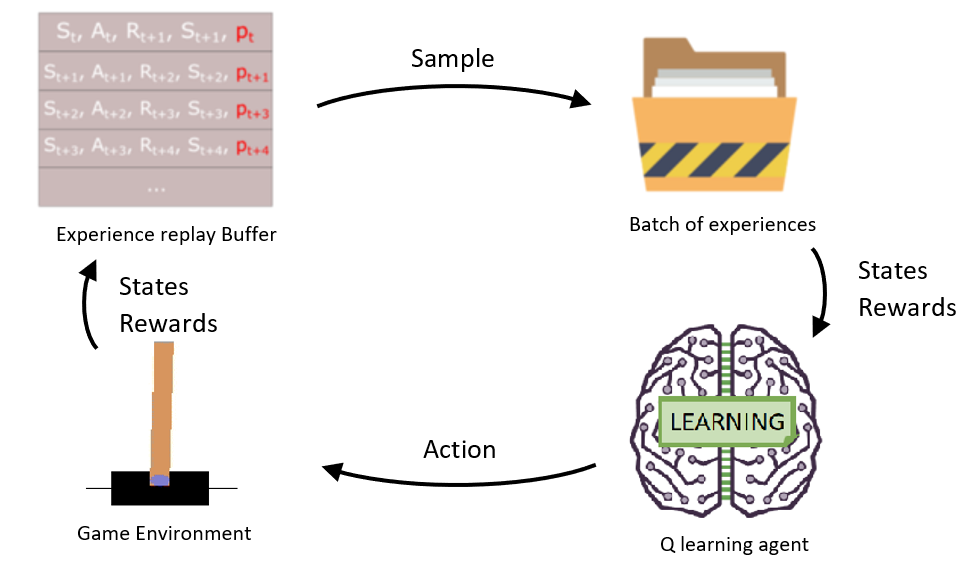
So, in our previous tutorial, we implemented the Double Dueling DQN Network model, and we saw that our agent improved this way slightly. Now it's time to implement Prioritized Experience Replay (PER), introduced in 2015 by Tom Schaul. The paper idea is that some experiences may be more critical than others for our training but might occur less frequently.
Because we sample the batch uniformly (selecting the experiences randomly), these rich experiences that occur rarely have practically no chance of being selected.
That's why, with PER, we will try to change the sampling distribution by using a criterion to define the priority of each tuple of experience.
So, we want to take into priority experience where there is a big difference between our prediction and the TD target since we have a lot to learn about it.
We'll use the absolute value of the magnitude of our TD error:
Here:
|δt| - Magnitude of our TD error;
e - constant assures that no experience has 0 probability of being taken.
Then we'll put priority to the experience of each replay buffer:
 But we can't do greedy prioritization because it will lead to constantly training the same experiences (that have big priority), and then we'll be over-fitting our agent. So, we will use stochastic prioritization, which generates the probability of being chosen for a replay:
But we can't do greedy prioritization because it will lead to constantly training the same experiences (that have big priority), and then we'll be over-fitting our agent. So, we will use stochastic prioritization, which generates the probability of being chosen for a replay:
Here:
pi - Priority value;
∑kpk - Normalization by all priority values in Replay Buffer;
a - Hyperparameter used to reintroduce some randomness in the experience selection for the replay buffer (if a=0 pure randomness, if a=1 only selects the experience with the highest priorities).
Consequently, during each time step, we will get a batch of samples with a batch probability distribution, and we'll train our network on it. But we still have a problem here. With a regular Experience Replay (deque) buffer, we use a stochastic update rule. Therefore, the way we sample the experiences must match the underlying distribution they came from.
When we have a regular (deque) experience, we select our experiences in a normal distribution — simply put, we choose our experiences randomly. There is no bias because each experience has the same chance to update our weights. But, because we use priority sampling, purely random sampling is abandoned. Therefore, we introduce a bias toward high-priority samples here (they have more chances to be selected).
If we would update our weights normally, we have a risk of over-fitting our agent. Samples with high priority are likely to be used for training many times compared to low priority experiences (= bias). So, as a consequence, we'll update our weights with only a tiny portion of experiences that we consider to be interesting.
To correct this bias, we'll use importance sampling weights (IS) that will adjust the updating by reducing the weights of the often seen samples:
Here:
N - Replay Buffer Size;
P(i) - Sampling probability.
The weights corresponding to high-priority samples have a minor adjustment (because the network will often see these experiences). In contrast, those corresponding to low-priority samples will have a full update.
The role of bias is to control how much these important sampling weights affect learning. In practice, the bias parameter is annealed up to one for the training because these weights are more important at the end of learning when our q values begin to converge. The unbiased nature of updates is most important near convergence.
Implementation
This time, the implementation will be a little bit fancier than before.
First, we can't just implement PER by sorting all the Experience Replay Buffers according to their priorities. This will not be efficient due to O(nlogn) for insertion and O(n) for sampling.
This article explains that we need to use another data structure instead of sorting an array — an unsorted sumtree.
A sumtree is a Binary Tree, a tree with only a maximum of two children for each node. The leaves (deepest nodes) contain the priority values, and a data array that points to leaves contains the experiences:
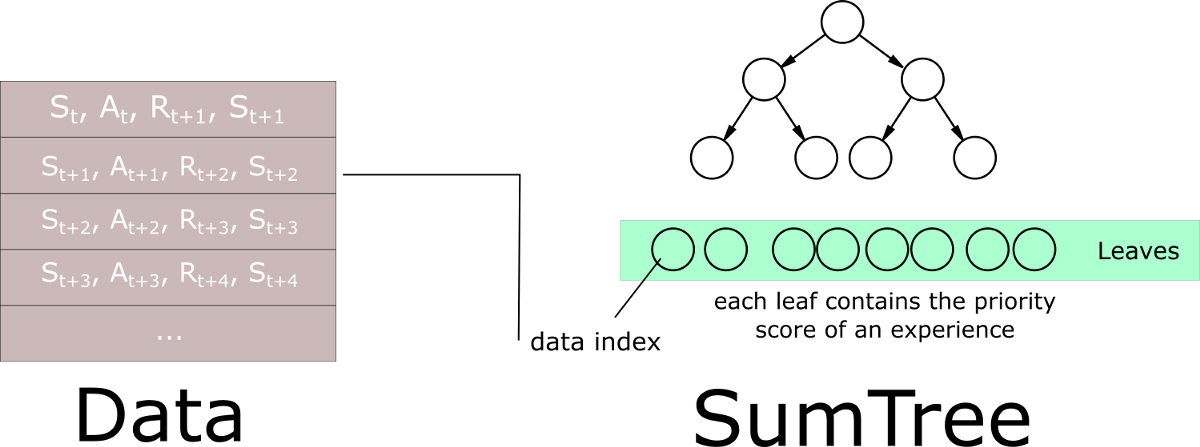
Then, we create a memory object that will contain our sumtree and data.
Next, to sample a minibatch of size k, the range [0, total_priority] will be divided into k ranges. A value is uniformly sampled from each range.
Finally, the transitions (experiences) that correspond to these sampled values are retrieved from the sumtree.
I will use the Morvan Zhou SumTree code from this link. So, first, we create a SumTree object class:
class SumTree(object):
data_pointer = 0
# Here we initialize the tree with all nodes = 0, and initialize the data with all values = 0
def __init__(self, capacity):
# Number of leaf nodes (final nodes) that contains experiences
self.capacity = capacity
# Generate the tree with all nodes values = 0
# To understand this calculation (2 * capacity - 1) look at the schema below
# Remember we are in a binary node (each node has max 2 children) so 2x size of leaf (capacity) - 1 (root node)
# Parent nodes = capacity - 1
# Leaf nodes = capacity
self.tree = np.zeros(2 * capacity - 1)
# Contains the experiences (so the size of data is capacity)
self.data = np.zeros(capacity, dtype=object)First, we want to build a tree with all nodes = 0 and initialize the data with all values = 0. So, we define several leaf nodes (final nodes) that contain experiences. Next, with self.tree = np.zeros(2 * capacity - 1) line we generate the tree with all nodes values = 0. To understand this calculation (2 * capacity - 1), look at the schema below:
0
/ \
0 0
/ \ / \
0 0 0 0 Here we are in a binary node (each node has max two children), so 2x size of the leaf (capacity) - 1 (root node). So, to calculate all nodes: Parent nodes = capacity - 1 and Leaf nodes = capacity. Finally, we define our data that contains the experiences (so the data size is capacity).
Second, we define add a function that will add our priority score in the sumtree leaf and add the experience in data:
def add(self, priority, data):
# Look at what index we want to put the experience
tree_index = self.data_pointer + self.capacity - 1
""" tree:
0
/ \
0 0
/ \ / \
tree_index 0 0 0 We fill the leaves from left to right
"""
# Update data frame
self.data[self.data_pointer] = data
# Update the leaf
self.update (tree_index, priority)
# Add 1 to data_pointer
self.data_pointer += 1
if self.data_pointer >= self.capacity: # If we're above the capacity, we go back to first index (we overwrite)
self.data_pointer = 0While putting new data to our tree, we fill the leaves from left to right, so first what we do is we look at what index we want to put the experience:
tree_index = self.data_pointer + self.capacity - 1
this is how our tree will look like while we start filling it:
0
/ \
0 0
/ \ / \
tree_index 0 0 0so, while adding new information to our tree, we are doing three steps:
- Update data frame:
self.data[self.data_pointer] = data; - We update the leaf:
self.update (tree_index, priority)- this function will be created later; - And we shift our pointer to the right by one:
self.data_pointer += 1.
If we reach the capacity limit, we go back to the first index (we overwrite) again.
As I said; next, we create a function to update the leaf priority score and propagate the change through the tree:
def update(self, tree_index, priority):
# Change = new priority score - former priority score
change = priority - self.tree[tree_index]
self.tree[tree_index] = priority
# then propagate the change through tree
# this method is faster than the recursive loop
while tree_index != 0:
tree_index = (tree_index - 1) // 2
self.tree[tree_index] += changeIn the update function, first, what we do is, calculate priority change. We subtract our previous priority score from the new priority, and we overwrite our last priority with a new one. After that, we propagate the change through the tree in a while loop.
Here is how our tree looks with six leaves:
0
/ \
1 2
/ \ / \
3 4 5 [6] The numbers in this tree are the indexes, not the priority values, so here we want to access the line above the leaves. So, for example: If we are in a leaf at index 6, we updated the priority score, then we need to update the index 2 nodes:
tree_index = (tree_index - 1) // 2
tree_index = (6-1)//2
tree_index = 2 # (because of // we round the result)the last step is to update our tree leaf with calculated change: self.tree[2] += change
Next, we must build a function to get a leaf from our tree. So, we'll create a function to get the leaf_index, priority value of that leaf, and experience associated with that leaf index:
def get_leaf(self, v):
parent_index = 0
while True:
left_child_index = 2 * parent_index + 1
right_child_index = left_child_index + 1
# If we reach bottom, end the search
if left_child_index >= len(self.tree):
leaf_index = parent_index
break
else: # downward search, always search for a higher priority node
if v <= self.tree[left_child_index]:
parent_index = left_child_index
else:
v -= self.tree[left_child_index]
parent_index = right_child_index
data_index = leaf_index - self.capacity + 1
return leaf_index, self.tree[leaf_index], self.data[data_index]
@property
def total_priority(self):
return self.tree[0] # Returns the root node To understand what we are doing, let's look at our tree from an index perspective:
0 -> storing priority sum
/ \
1 2
/ \ / \
3 4 5 6 -> storing priority for experiencesHere we are looping our code in a while loop. The first thing we do, we find our left and right child indexes. We keep repeating the action to find our leaf until we see it. When we know our parent leaf index, we calculate our data index, and finally, we return our leaf index, our leaf priority, and data stored in according leaf index.
In the end, I also wrote the total_priority function and this function will be used to return the root node.
Now we finished constructing our SumTree object; next, we'll build a memory object. Writing this tutorial, I relied on code from this link. So same as before, we'll create a Memory object:
class Memory(object): # stored as ( state, action, reward, next_state ) in SumTree
PER_e = 0.01 # Hyperparameter that we use to avoid some experiences to have 0 probability of being taken
PER_a = 0.6 # Hyperparameter that we use to make a tradeoff between taking only exp with high priority and sampling randomly
PER_b = 0.4 # importance-sampling, from initial value increasing to 1
PER_b_increment_per_sampling = 0.001
absolute_error_upper = 1. # clipped abs error
def __init__(self, capacity):
# Making the tree
self.tree = SumTree(capacity)Here we defined three hyperparameters:
- PER_e, hyperparameter that we use to avoid some experiences to have 0 probability of being taken;
- PER_a, hyperparameter that we use to make a tradeoff between taking the only experience with high priority and sampling randomly;
- PER_b, importance-sampling, from the initial value, increasing to 1.
Before, we created a tree function composed of a sumtree that contains the priority scores at his leaf and data in an array. We won't use deque() differently from our previous tutorials because our experiences index changes by one at each timestep. We prefer to use a simple array and overwrite it when our memory is full.
Next, we define a function to store a new experience in our tree. Each unique experience will have a score of max_prority (it will be improved when we use this experience to train our agent). Experience, f. e. in Cartpole game, would be (state, action, reward, next_state, done). So, we are defining our store function:
def store(self, experience):
# Find the max priority
max_priority = np.max(self.tree.tree[-self.tree.capacity:])
# If the max priority = 0 we can't put priority = 0 since this experience will never have a chance to be selected
# So we use a minimum priority
if max_priority == 0:
max_priority = self.absolute_error_upper
self.tree.add(max_priority, experience) # set the max priority for new prioritySo, here we search for max priority in our leaf nodes that contain experiences. If we can't find any priority in our tree, we set a max priority as absolute_error_upper, in our case 1. Then we store this priority and experience in our memory tree. Else wise we keep our experience with the maximum priority we can find.
Next, we create a sample function that will pick a batch from our tree memory used to train our model. First, we sample a minibatch of n size, the range [0, priority_total], into priority ranges. Then a value is uniformly sampled from each range. Then we search in the sumtree for the experience where the priority score corresponds to retrieved sample values.
def sample(self, n):
# Create a minibatch array that will contains the minibatch
minibatch = []
b_idx = np.empty((n,), dtype=np.int32)
# Calculate the priority segment
# Here, as explained in the paper, we divide the Range[0, ptotal] into n ranges
priority_segment = self.tree.total_priority / n # priority segment
for i in range(n):
# A value is uniformly sample from each range
a, b = priority_segment * i, priority_segment * (i + 1)
value = np.random.uniform(a, b)
# Experience that correspond to each value is retrieved
index, priority, data = self.tree.get_leaf(value)
b_idx[i]= index
minibatch.append([data[0],data[1],data[2],data[3],data[4]])
return b_idx, minibatchAnd finally, we create a function to update the priorities on the tree:
def batch_update(self, tree_idx, abs_errors):
abs_errors += self.PER_e # convert to abs and avoid 0
clipped_errors = np.minimum(abs_errors, self.absolute_error_upper)
ps = np.power(clipped_errors, self.PER_a)
for ti, p in zip(tree_idx, ps):
self.tree.update(ti, p)Now we finished our Memory and SumTree classes, don't worry, everything is uploaded to GitHub so that you could download this code! The above code is in the PER.py script.
Now we can continue on our main agent code. We'll modify it to use deque() and prioritized memory replay with a simple Boolean function; this will help us check the difference in results.
An agent with Prioritized Experience Replay
So, now we know how our Prioritized Experienced Replay memory works, so I stored our created SumTree and Memory object classes to PER.py script. We'll import them with the following new line: from PER import *.
In our DQN Agent initialization, we create an object self.MEMORY = Memory(memory_size) with memory_size = 10000. So while we will be using PER memory instead of self. memory = deque(maxlen=2000) we'll use self. MEMORY. And to easily control if we want to use PER or not to use it, we'll insert self.USE_PER = True Boolean command.
Note: all this memory_size = 10000 is stored in memory; if you have a too large number here, you may get out of memory. So, while implementing PER, almost all the functions stay the same as before; only a few of them change a little. For example, now remember function will look like this:
def remember(self, state, action, reward, next_state, done):
experience = state, action, reward, next_state, done
if self.USE_PER:
self.MEMORY.store(experience)
else:
self.memory.append((experience))As I already said, here, we choose what memory type our agent will use with the Boolean operation.
More will change our replay function (how we sample our minibatches); we take them from PER memory or the DEQ list. If we take our mini-batches from PER, we must recalculate absolute_errors and update our memory with it.
def replay(self):
if self.USE_PER:
# Sample minibatch from the PER memory
tree_idx, minibatch = self.MEMORY.sample(self.batch_size)
else:
# Randomly sample minibatch from the deque memory
minibatch = random.sample(self.memory, min(len(self.memory), self.batch_size))
'''
everything stay the same here as before
'''
target_old = np.array(target)
'''
everything stay the same here as before
'''
if self.USE_PER:
absolute_errors = np.abs(target_old[i]-target[i])
# Update priority
self.MEMORY.batch_update(tree_idx, absolute_errors)
# Train the Neural Network with batches
self.model.fit(state, target, batch_size=self.batch_size, verbose=0)Our run function doesn't change. From this point, you should download the code from the above GitHub link.
# Tutorial by www.pylessons.com
# Tutorial written for - Tensorflow 1.15, Keras 2.2.4
import os
import random
import gym
import pylab
import numpy as np
from collections import deque
from keras.models import Model, load_model
from keras.layers import Input, Dense, Lambda, Add
from keras.optimizers import Adam, RMSprop
from keras import backend as K
from PER import *
def OurModel(input_shape, action_space, dueling):
X_input = Input(input_shape)
X = X_input
# 'Dense' is the basic form of a neural network layer
# Input Layer of state size(4) and Hidden Layer with 512 nodes
X = Dense(512, input_shape=input_shape, activation="relu", kernel_initializer='he_uniform')(X)
# Hidden layer with 256 nodes
X = Dense(256, activation="relu", kernel_initializer='he_uniform')(X)
# Hidden layer with 64 nodes
X = Dense(64, activation="relu", kernel_initializer='he_uniform')(X)
if dueling:
state_value = Dense(1, kernel_initializer='he_uniform')(X)
state_value = Lambda(lambda s: K.expand_dims(s[:, 0], -1), output_shape=(action_space,))(state_value)
action_advantage = Dense(action_space, kernel_initializer='he_uniform')(X)
action_advantage = Lambda(lambda a: a[:, :] - K.mean(a[:, :], keepdims=True), output_shape=(action_space,))(action_advantage)
X = Add()([state_value, action_advantage])
else:
# Output Layer with # of actions: 2 nodes (left, right)
X = Dense(action_space, activation="linear", kernel_initializer='he_uniform')(X)
model = Model(inputs = X_input, outputs = X, name='CartPole D3QN model')
model.compile(loss="mean_squared_error", optimizer=RMSprop(lr=0.00025, rho=0.95, epsilon=0.01), metrics=["accuracy"])
model.summary()
return model
class DQNAgent:
def __init__(self, env_name):
self.env_name = env_name
self.env = gym.make(env_name)
self.env.seed(0)
# by default, CartPole-v1 has max episode steps = 500
self.env._max_episode_steps = 4000
self.state_size = self.env.observation_space.shape[0]
self.action_size = self.env.action_space.n
self.EPISODES = 1000
memory_size = 10000
self.MEMORY = Memory(memory_size)
self.memory = deque(maxlen=2000)
self.gamma = 0.95 # discount rate
# EXPLORATION HYPERPARAMETERS for epsilon and epsilon greedy strategy
self.epsilon = 1.0 # exploration probability at start
self.epsilon_min = 0.01 # minimum exploration probability
self.epsilon_decay = 0.0005 # exponential decay rate for exploration prob
self.batch_size = 32
# defining model parameters
self.ddqn = True # use doudle deep q network
self.Soft_Update = False # use soft parameter update
self.dueling = True # use dealing netowrk
self.epsilot_greedy = False # use epsilon greedy strategy
self.USE_PER = True
self.TAU = 0.1 # target network soft update hyperparameter
self.Save_Path = 'Models'
if not os.path.exists(self.Save_Path): os.makedirs(self.Save_Path)
self.scores, self.episodes, self.average = [], [], []
self.Model_name = os.path.join(self.Save_Path, self.env_name+"_e_greedy.h5")
# create main model and target model
self.model = OurModel(input_shape=(self.state_size,), action_space = self.action_size, dueling = self.dueling)
self.target_model = OurModel(input_shape=(self.state_size,), action_space = self.action_size, dueling = self.dueling)
# after some time interval update the target model to be same with model
def update_target_model(self):
if not self.Soft_Update and self.ddqn:
self.target_model.set_weights(self.model.get_weights())
return
if self.Soft_Update and self.ddqn:
q_model_theta = self.model.get_weights()
target_model_theta = self.target_model.get_weights()
counter = 0
for q_weight, target_weight in zip(q_model_theta, target_model_theta):
target_weight = target_weight * (1-self.TAU) + q_weight * self.TAU
target_model_theta[counter] = target_weight
counter += 1
self.target_model.set_weights(target_model_theta)
def remember(self, state, action, reward, next_state, done):
experience = state, action, reward, next_state, done
if self.USE_PER:
self.MEMORY.store(experience)
else:
self.memory.append((experience))
def act(self, state, decay_step):
# EPSILON GREEDY STRATEGY
if self.epsilot_greedy:
# Here we'll use an improved version of our epsilon greedy strategy for Q-learning
explore_probability = self.epsilon_min + (self.epsilon - self.epsilon_min) * np.exp(-self.epsilon_decay * decay_step)
# OLD EPSILON STRATEGY
else:
if self.epsilon > self.epsilon_min:
self.epsilon *= (1-self.epsilon_decay)
explore_probability = self.epsilon
if explore_probability > np.random.rand():
# Make a random action (exploration)
return random.randrange(self.action_size), explore_probability
else:
# Get action from Q-network (exploitation)
# Estimate the Qs values state
# Take the biggest Q value (= the best action)
return np.argmax(self.model.predict(state)), explore_probability
def replay(self):
if self.USE_PER:
tree_idx, minibatch = self.MEMORY.sample(self.batch_size)
else:
minibatch = random.sample(self.memory, min(len(self.memory), self.batch_size))
state = np.zeros((self.batch_size, self.state_size))
next_state = np.zeros((self.batch_size, self.state_size))
action, reward, done = [], [], []
# do this before prediction
# for speedup, this could be done on the tensor level
# but easier to understand using a loop
for i in range(self.batch_size):
state[i] = minibatch[i][0]
action.append(minibatch[i][1])
reward.append(minibatch[i][2])
next_state[i] = minibatch[i][3]
done.append(minibatch[i][4])
# do batch prediction to save speed
# predict Q-values for starting state using the main network
target = self.model.predict(state)
target_old = np.array(target)
# predict best action in ending state using the main network
target_next = self.model.predict(next_state)
# predict Q-values for ending state using the target network
target_val = self.target_model.predict(next_state)
for i in range(len(minibatch)):
# correction on the Q value for the action used
if done[i]:
target[i][action[i]] = reward[i]
else:
if self.ddqn: # Double - DQN
# current Q Network selects the action
# a'_max = argmax_a' Q(s', a')
a = np.argmax(target_next[i])
# target Q Network evaluates the action
# Q_max = Q_target(s', a'_max)
target[i][action[i]] = reward[i] + self.gamma * (target_val[i][a])
else: # Standard - DQN
# DQN chooses the max Q value among next actions
# selection and evaluation of action is on the target Q Network
# Q_max = max_a' Q_target(s', a')
target[i][action[i]] = reward[i] + self.gamma * (np.amax(target_next[i]))
if self.USE_PER:
indices = np.arange(self.batch_size, dtype=np.int32)
absolute_errors = np.abs(target_old[indices, np.array(action)]-target[indices, np.array(action)])
# Update priority
self.MEMORY.batch_update(tree_idx, absolute_errors)
# Train the Neural Network with batches
self.model.fit(state, target, batch_size=self.batch_size, verbose=0)
def load(self, name):
self.model = load_model(name)
def save(self, name):
self.model.save(name)
pylab.figure(figsize=(18, 9))
def PlotModel(self, score, episode):
self.scores.append(score)
self.episodes.append(episode)
self.average.append(sum(self.scores[-50:]) / len(self.scores[-50:]))
pylab.plot(self.episodes, self.average, 'r')
pylab.plot(self.episodes, self.scores, 'b')
pylab.ylabel('Score', fontsize=18)
pylab.xlabel('Steps', fontsize=18)
dqn = 'DQN_'
softupdate = ''
dueling = ''
greedy = ''
PER = ''
if self.ddqn: dqn = 'DDQN_'
if self.Soft_Update: softupdate = '_soft'
if self.dueling: dueling = '_Dueling'
if self.epsilot_greedy: greedy = '_Greedy'
if self.USE_PER: PER = '_PER'
try:
pylab.savefig(dqn+self.env_name+softupdate+dueling+greedy+PER+".png")
except OSError:
pass
return str(self.average[-1])[:5]
def run(self):
decay_step = 0
for e in range(self.EPISODES):
state = self.env.reset()
state = np.reshape(state, [1, self.state_size])
done = False
i = 0
while not done:
#self.env.render()
decay_step += 1
action, explore_probability = self.act(state, decay_step)
next_state, reward, done, _ = self.env.step(action)
next_state = np.reshape(next_state, [1, self.state_size])
if not done or i == self.env._max_episode_steps-1:
reward = reward
else:
reward = -100
self.remember(state, action, reward, next_state, done)
state = next_state
i += 1
if done:
# every step update target model
self.update_target_model()
# every episode, plot the result
average = self.PlotModel(i, e)
print("episode: {}/{}, score: {}, e: {:.2}, average: {}".format(e, self.EPISODES, i, explore_probability, average))
if i == self.env._max_episode_steps:
print("Saving trained model to", self.Model_name)
#self.save(self.Model_name)
break
self.replay()
self.env.close()
def test(self):
self.load(self.Model_name)
for e in range(self.EPISODES):
state = self.env.reset()
state = np.reshape(state, [1, self.state_size])
done = False
i = 0
while not done:
self.env.render()
action = np.argmax(self.model.predict(state))
next_state, reward, done, _ = self.env.step(action)
state = np.reshape(next_state, [1, self.state_size])
i += 1
if done:
print("episode: {}/{}, score: {}".format(e, self.EPISODES, i))
break
if __name__ == "__main__":
env_name = 'CartPole-v1'
agent = DQNAgent(env_name)
agent.run()
#agent.test()Now, look at two examples of the same CartPole balancing game, where I trained our agent for 1000 steps. I trained two models:
- One with PER enabled;
- Another with PER disabled.
Both agents were trained with double dueling Deep Q Network, epsilon greedy update, and soft update disabled.
First, let's look at our results, where we were training our agent without PER. Results look very similar to what they were in my previous tutorial. The best average score our agent could hit was around 1060:
.png) Now let's look at our agent while it was using Prioritized Experienced Replay memory:
Now let's look at our agent while it was using Prioritized Experienced Replay memory:
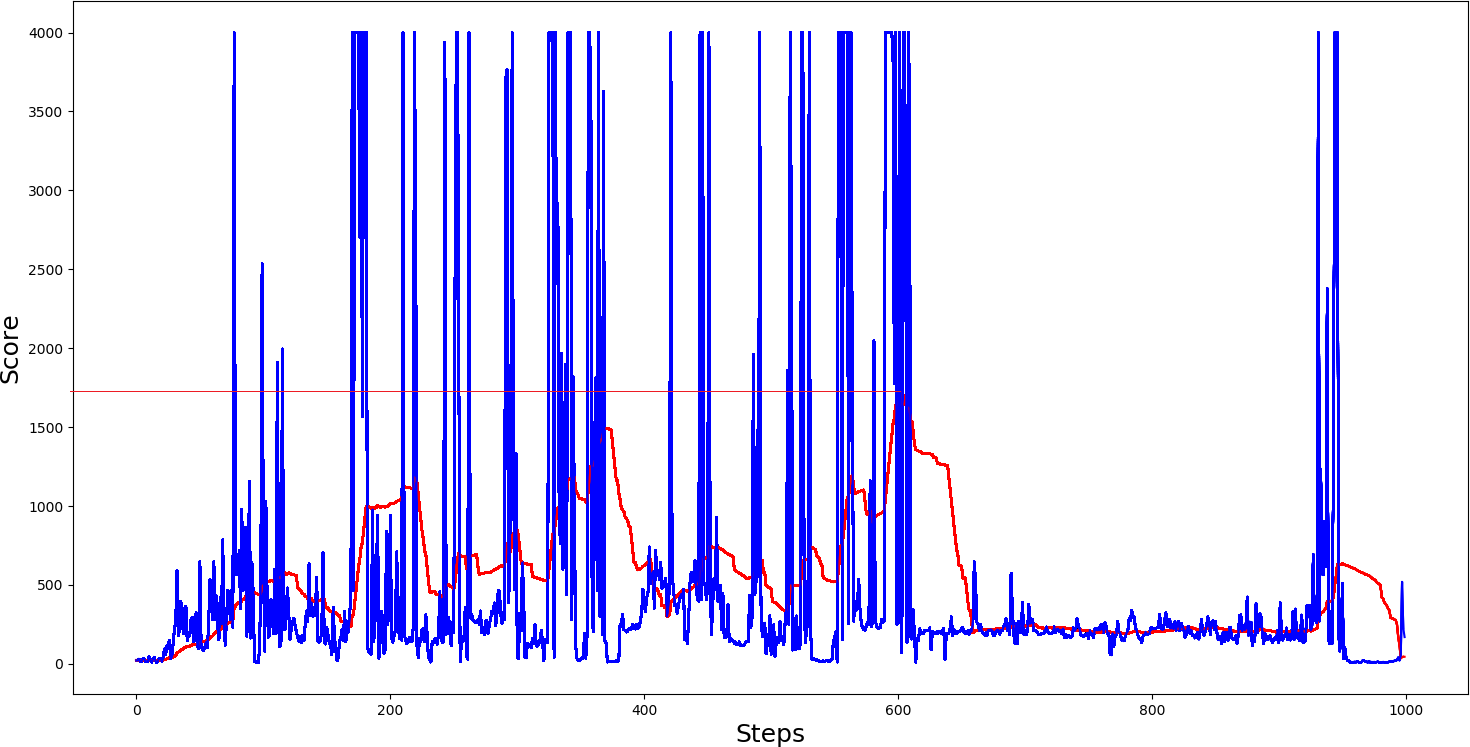
Conclusion:
As we can see, the difference is as day and night, our 50 steps moving average was close somewhere around 1750 points per game, while without PER, our average score was a little more than 1000. We can say that performance showed that PER translates into faster learning and higher performance from these graphs. What's more, it's complementary to D3QN. If we would train our agent for much longer and with a larger prioritized memory buffer, maybe it would reach even better results, who knows.
So, up to this point, we were working with quite a simple environment (only four state variables), and we were able quite fast to train our agent. Now let's take this agent to the next level and introduce our agent with 3D image data. So, if you want to see how we'll do that, see you in the next tutorial.