There's a massive difference between reading about Reinforcement Learning and implementing it. In this tutorial, I'll implement a Deep Neural Network for Reinforcement Learning (Deep Q Network), and we will see it learns and finally becomes good enough to beat the computer in Pong!
By the end of this post, you'll be able to do the following:
- Write a Neural Network from scratch;
- Implement a Deep Q Network with Reinforcement Learning;
- Build an A.I. for Pong that can beat the computer in less than 300 lines of Python;
- Use OpenAI gym.
Considering the limited time and for learning purposes, I am not aiming for a perfect trained agent. Still, I hope this project could help people get familiar with the basic process of DQN algorithms and Keras. The following tutorial took two days for four different agents to learn on a computer with GPU. A lot more training and tuning are required to obtain production results, which is not my focus.
Tutorial Prerequisites: familiarity with Neural Networks, supervised learning, Tensorflow 1.15, Keras 2.2.4, OpenAI gym.
This tutorial is a part of my previous tutorials. I use my previous tutorial code structure - this way, it's easier to understand line by line when you start learning from the first tutorial part. I should mention that there won't be a theory in this tutorial because we already covered all the approaches we need in previous tutorials. We will change several lines of code that our Network would learn to play Pong instead of Cartpole.
Setup:
- Open up the code to follow along and copy or clone it;
- Follow the instructions for installing OpenAI Gym. You may need to install CMake first;
- Run
pip install gym[atari]; - Let's get to the next part.
We are given the following problems:
- A sequence of images (frames) representing each frame of the Pong game;
- An indication of when we've won or lost the game;
- An opponent agent that is the traditional Pong computer player;
An agent we control that we can tell to do one step out of 6 at each frame.
Can we use these pieces to train our agent to beat the computer? Moreover, can we make our solution good enough to be reused to win in games that aren't Pong?
Solution:
Indeed, we can! We'll do this by building a Neural Network that takes in each image and outputs a command to our A.I. to take the correct move.
We can break this down into the following steps:
- Take in images from the game and preprocess it (remove color, background, down-sample, etc.);
- Use the Neural Network to compute a probability of taking the correct action;
- Sample from that probability distribution and tell the agent to move up, down, or stay in the same position;
- If the round is over (you missed the ball or the opponent missed the ball), find whether you won or lost;
- When the episode has finished(someone got to 21 points), pass the result through the training algorithm;
- Repeat this process until our agent is tuned to the point where we can beat the computer. That's it! Let’s start looking at how our code achieves this.
Ok, now that we’ve described the problem and its solution, let’s get to writing some code (Details in YouTube tutorial)!
Code:
You can check the complete Video tutorial code and download trained models on GitHub.
# Tutorial by www.pylessons.com
# Tutorial written for - Tensorflow 1.15, Keras 2.2.4
import os
import random
import gym
import pylab
import numpy as np
from collections import deque
from keras.models import Model, load_model
from keras.layers import Input, Dense, Lambda, Add, Conv2D, Flatten
from keras.optimizers import Adam, RMSprop
from keras import backend as K
from PER import *
import cv2
def OurModel(input_shape, action_space, dueling):
X_input = Input(input_shape)
X = X_input
#X = Conv2D(64, 5, strides=(3, 3),padding="valid", input_shape=input_shape, activation="relu", data_format="channels_first")(X)
X = Conv2D(32, 8, strides=(4, 4),padding="valid", input_shape=input_shape, activation="relu", data_format="channels_first")(X)
X = Conv2D(64, 4, strides=(2, 2),padding="valid", activation="relu", data_format="channels_first")(X)
X = Conv2D(64, 3, strides=(1, 1),padding="valid", activation="relu", data_format="channels_first")(X)
X = Flatten()(X)
# 'Dense' is the basic form of a neural network layer
X = Dense(512, activation="relu", kernel_initializer='he_uniform')(X)
X = Dense(256, activation="relu", kernel_initializer='he_uniform')(X)
X = Dense(64, activation="relu", kernel_initializer='he_uniform')(X)
if dueling:
state_value = Dense(1, kernel_initializer='he_uniform')(X)
state_value = Lambda(lambda s: K.expand_dims(s[:, 0], -1), output_shape=(action_space,))(state_value)
action_advantage = Dense(action_space, kernel_initializer='he_uniform')(X)
action_advantage = Lambda(lambda a: a[:, :] - K.mean(a[:, :], keepdims=True), output_shape=(action_space,))(action_advantage)
X = Add()([state_value, action_advantage])
else:
# Output Layer with # of actions: 2 nodes (left, right)
X = Dense(action_space, activation="linear", kernel_initializer='he_uniform')(X)
model = Model(inputs = X_input, outputs = X)
model.compile(optimizer=Adam(lr=0.00005), loss='mean_squared_error')
model.summary()
return model
class DQNAgent:
def __init__(self, env_name):
self.env_name = env_name
self.env = gym.make(env_name)
#self.env.seed(0)
self.action_size = self.env.action_space.n
self.EPISODES = 1000
# Instantiate memory
memory_size = 25000
self.MEMORY = Memory(memory_size)
self.memory = deque(maxlen=memory_size)
self.gamma = 0.99 # discount rate
# EXPLORATION HYPERPARAMETERS for epsilon and epsilon greedy strategy
self.epsilon = 1.0 # exploration probability at start
self.epsilon_min = 0.02 # minimum exploration probability
self.epsilon_decay = 0.00002 # exponential decay rate for exploration prob
self.batch_size = 32
# defining model parameters
self.ddqn = False # use doudle deep q network
self.dueling = False # use dealing network
self.epsilon_greedy = False # use epsilon greedy strategy
self.USE_PER = False # use priority experienced replay
self.Save_Path = 'Models'
if not os.path.exists(self.Save_Path): os.makedirs(self.Save_Path)
self.scores, self.episodes, self.average = [], [], []
self.Model_name = os.path.join(self.Save_Path, self.env_name+"_CNN.h5")
self.ROWS = 80
self.COLS = 80
self.REM_STEP = 4
self.update_model_steps = 1000
self.state_size = (self.REM_STEP, self.ROWS, self.COLS)
self.image_memory = np.zeros(self.state_size)
# create main model and target model
self.model = OurModel(input_shape=self.state_size, action_space = self.action_size, dueling = self.dueling)
self.target_model = OurModel(input_shape=self.state_size, action_space = self.action_size, dueling = self.dueling)
# after some time interval update the target model to be same with model
def update_target_model(self, game_steps):
if game_steps % self.update_model_steps == 0:
self.target_model.set_weights(self.model.get_weights())
return
def remember(self, state, action, reward, next_state, done):
experience = state, action, reward, next_state, done
if self.USE_PER:
self.MEMORY.store(experience)
else:
self.memory.append((experience))
def act(self, state, decay_step):
# EPSILON GREEDY STRATEGY
if self.epsilon_greedy:
# Here we'll use an improved version of our epsilon greedy strategy for Q-learning
explore_probability = self.epsilon_min + (self.epsilon - self.epsilon_min) * np.exp(-self.epsilon_decay * decay_step)
# OLD EPSILON STRATEGY
else:
if self.epsilon > self.epsilon_min:
self.epsilon *= (1-self.epsilon_decay)
explore_probability = self.epsilon
if explore_probability > np.random.rand():
# Make a random action (exploration)
return random.randrange(self.action_size), explore_probability
else:
# Get action from Q-network (exploitation)
# Estimate the Qs values state
# Take the biggest Q value (= the best action)
return np.argmax(self.model.predict(state)), explore_probability
def replay(self):
if self.USE_PER:
# Sample minibatch from the PER memory
tree_idx, minibatch = self.MEMORY.sample(self.batch_size)
else:
if len(self.memory) > self.batch_size:
# Randomly sample minibatch from the deque memory
minibatch = random.sample(self.memory, self.batch_size)
else:
return
state = np.zeros((self.batch_size, *self.state_size), dtype=np.float32)
action = np.zeros(self.batch_size, dtype=np.int32)
reward = np.zeros(self.batch_size, dtype=np.float32)
next_state = np.zeros((self.batch_size, *self.state_size), dtype=np.float32)
done = np.zeros(self.batch_size, dtype=np.uint8)
# do this before prediction
# for speedup, this could be done on the tensor level
# but easier to understand using a loop
for i in range(len(minibatch)):
state[i], action[i], reward[i], next_state[i], done[i] = minibatch[i]
# do batch prediction to save speed
# predict Q-values for starting state using the main network
target = self.model.predict(state)
target_old = np.array(target)
# predict best action in ending state using the main network
target_next = self.model.predict(next_state)
# predict Q-values for ending state using the target network
target_val = self.target_model.predict(next_state)
for i in range(len(minibatch)):
# correction on the Q value for the action used
if done[i]:
target[i][action[i]] = reward[i]
else:
# the key point of Double DQN
# selection of action is from model
# update is from target model
if self.ddqn: # Double - DQN
# current Q Network selects the action
# a'_max = argmax_a' Q(s', a')
a = np.argmax(target_next[i])
# target Q Network evaluates the action
# Q_max = Q_target(s', a'_max)
target[i][action[i]] = reward[i] + self.gamma * target_val[i][a]
else: # Standard - DQN
# DQN chooses the max Q value among next actions
# selection and evaluation of action is on the target Q Network
# Q_max = max_a' Q_target(s', a')
# when using target model in simple DQN rules, we get better performance
target[i][action[i]] = reward[i] + self.gamma * np.amax(target_val[i])
if self.USE_PER:
indices = np.arange(self.batch_size, dtype=np.int32)
absolute_errors = np.abs(target_old[indices, action]-target[indices, action])
# Update priority
self.MEMORY.batch_update(tree_idx, absolute_errors)
# Train the Neural Network with batches
self.model.fit(state, target, batch_size=self.batch_size, verbose=0)
def load(self, name):
self.model = load_model()
def save(self, name):
self.model.save(name)
pylab.figure(figsize=(18, 9))
def PlotModel(self, score, episode):
self.scores.append(score)
self.episodes.append(episode)
self.average.append(sum(self.scores[-50:]) / len(self.scores[-50:]))
pylab.plot(self.episodes, self.average, 'r')
pylab.plot(self.episodes, self.scores, 'b')
pylab.ylabel('Score', fontsize=18)
pylab.xlabel('Games', fontsize=18)
dqn = 'DQN_'
dueling = ''
greedy = ''
PER = ''
if self.ddqn: dqn = '_DDQN'
if self.dueling: dueling = '_Dueling'
if self.epsilon_greedy: greedy = '_Greedy'
if self.USE_PER: PER = '_PER'
try:
pylab.savefig(self.env_name+dqn+dueling+greedy+PER+"_CNN.png")
except OSError:
pass
# no need to worry about model, when doing a lot of experiments
self.Model_name = os.path.join(self.Save_Path, self.env_name+dqn+dueling+greedy+PER+"_CNN.h5")
return self.average[-1]
def imshow(self, image, rem_step=0):
cv2.imshow("cartpole"+str(rem_step), image[rem_step,...])
if cv2.waitKey(25) & 0xFF == ord("q"):
cv2.destroyAllWindows()
return
def GetImage(self, frame):
self.env.render()
# croping frame to 80x80 size
frame_cropped = frame[35:195:2, ::2,:]
if frame_cropped.shape[0] != self.COLS or frame_cropped.shape[1] != self.ROWS:
# OpenCV resize function
frame_cropped = cv2.resize(frame, (self.COLS, self.ROWS), interpolation=cv2.INTER_CUBIC)
# converting to RGB (numpy way)
frame_rgb = 0.299*frame_cropped[:,:,0] + 0.587*frame_cropped[:,:,1] + 0.114*frame_cropped[:,:,2]
# converting to RGB (OpenCV way)
#frame_rgb = cv2.cvtColor(frame_cropped, cv2.COLOR_RGB2GRAY)
# dividing by 255 we expresses value to 0-1 representation
new_frame = np.array(frame_rgb).astype(np.float32) / 255.0
# push our data by 1 frame, similar as deq() function work
self.image_memory = np.roll(self.image_memory, 1, axis = 0)
# inserting new frame to free space
self.image_memory[0,:,:] = new_frame
# show image frame
#self.imshow(self.image_memory,0)
#self.imshow(self.image_memory,1)
#self.imshow(self.image_memory,2)
#self.imshow(self.image_memory,3)
return np.expand_dims(self.image_memory, axis=0)
def reset(self):
frame = self.env.reset()
for i in range(self.REM_STEP):
state = self.GetImage(frame)
return state
def step(self,action):
next_state, reward, done, info = self.env.step(action)
next_state = self.GetImage(next_state)
return next_state, reward, done, info
def run(self):
decay_step = 0
max_average = -21.0
for e in range(self.EPISODES):
state = self.reset()
done = False
score = 0
SAVING = ''
while not done:
decay_step += 1
action, explore_probability = self.act(state, decay_step)
next_state, reward, done, _ = self.step(action)
self.remember(state, action, reward, next_state, done)
state = next_state
score += reward
if done:
# every episode, plot the result
average = self.PlotModel(score, e)
# saving best models
if average >= max_average:
max_average = average
self.save(self.Model_name)
SAVING = "SAVING"
else:
SAVING = ""
print("episode: {}/{}, score: {}, e: {:.2f}, average: {:.2f} {}".format(e, self.EPISODES, score, explore_probability, average, SAVING))
# update target model
self.update_target_model(decay_step)
# train model
self.replay()
# close environemnt when finish training
self.env.close()
def test(self, Model_name):
self.load(Model_name)
for e in range(self.EPISODES):
state = self.reset()
done = False
score = 0
while not done:
self.env.render()
action = np.argmax(self.model.predict(state))
next_state, reward, done, _ = self.env.step(action)
score += reward
if done:
print("episode: {}/{}, score: {}".format(e, self.EPISODES, score))
break
self.env.close()
if __name__ == "__main__":
env_name = 'Pong-v0'
agent = DQNAgent(env_name)
#agent.run()
agent.test('Models/Pong-v0_DQN_CNN.h5')Results:
So I started to train the model from the simplest one, a simple Deep Q network. Parameters I used to use:
self.ddqn = False # use doudle deep q networks
self.dueling = False # use dealing network
self.USE_PER = False # use priority experienced replayI thought that this should be trained and that it will perform the worst. The maximum average score it could get was as close to 5 scores. But let us look at other models performance:
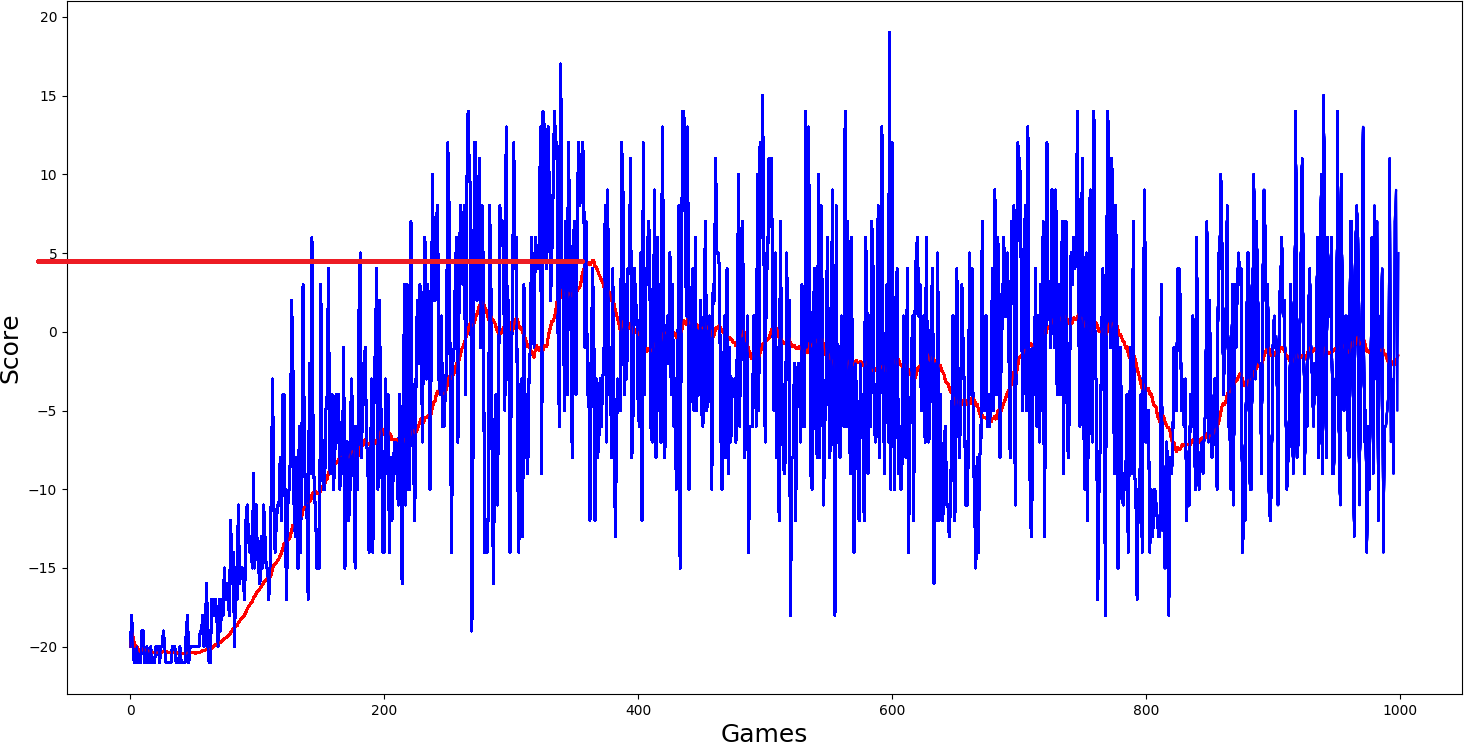
Ok, I thought, simple DQN model performed quite nice; I will add a double network to it self.ddqn = True and we'll see how it will work. But what I saw in my results was not satisfying me; it performed even worse:
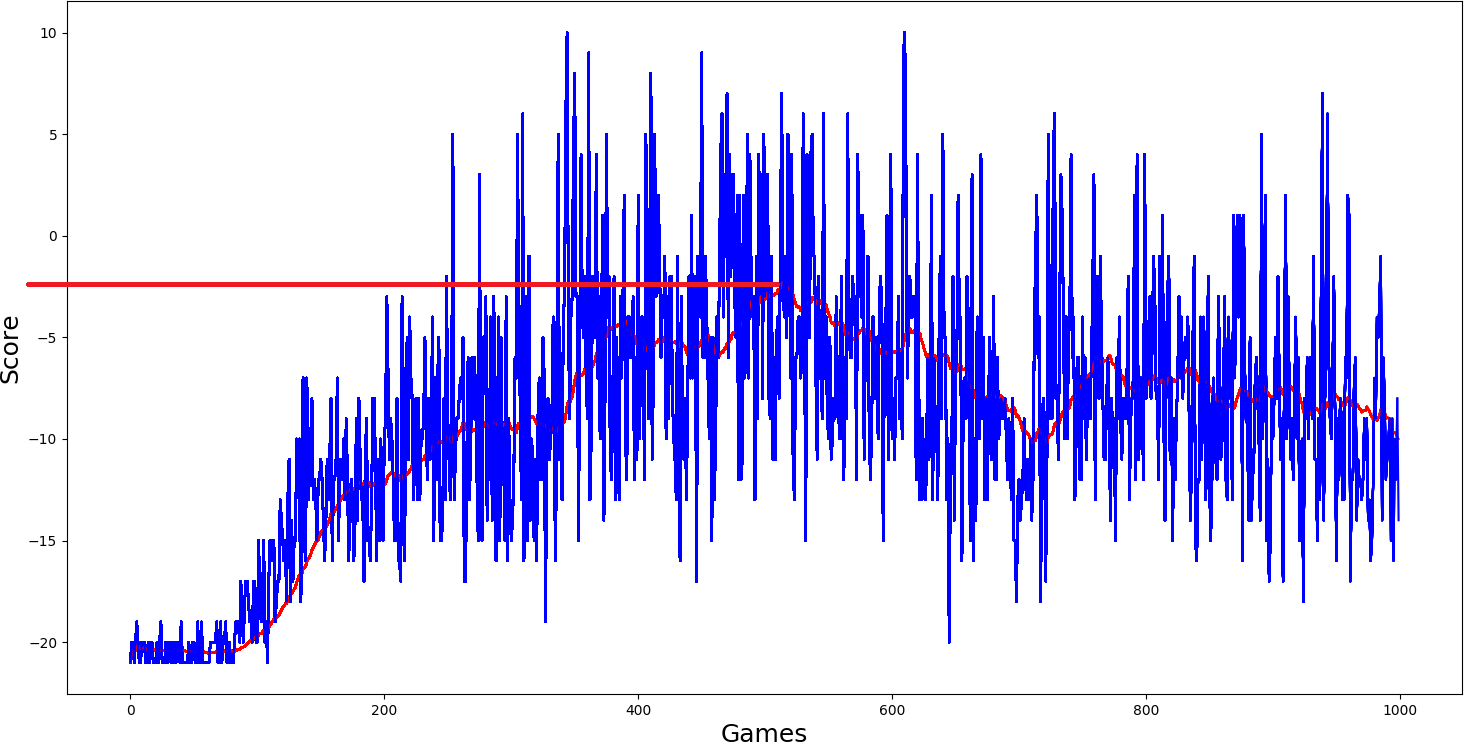
Then I added dueling self.dueling = True network, and I thought it should really get better than the two above-trained models. But results again were quite similar, average score just a little more than zero...
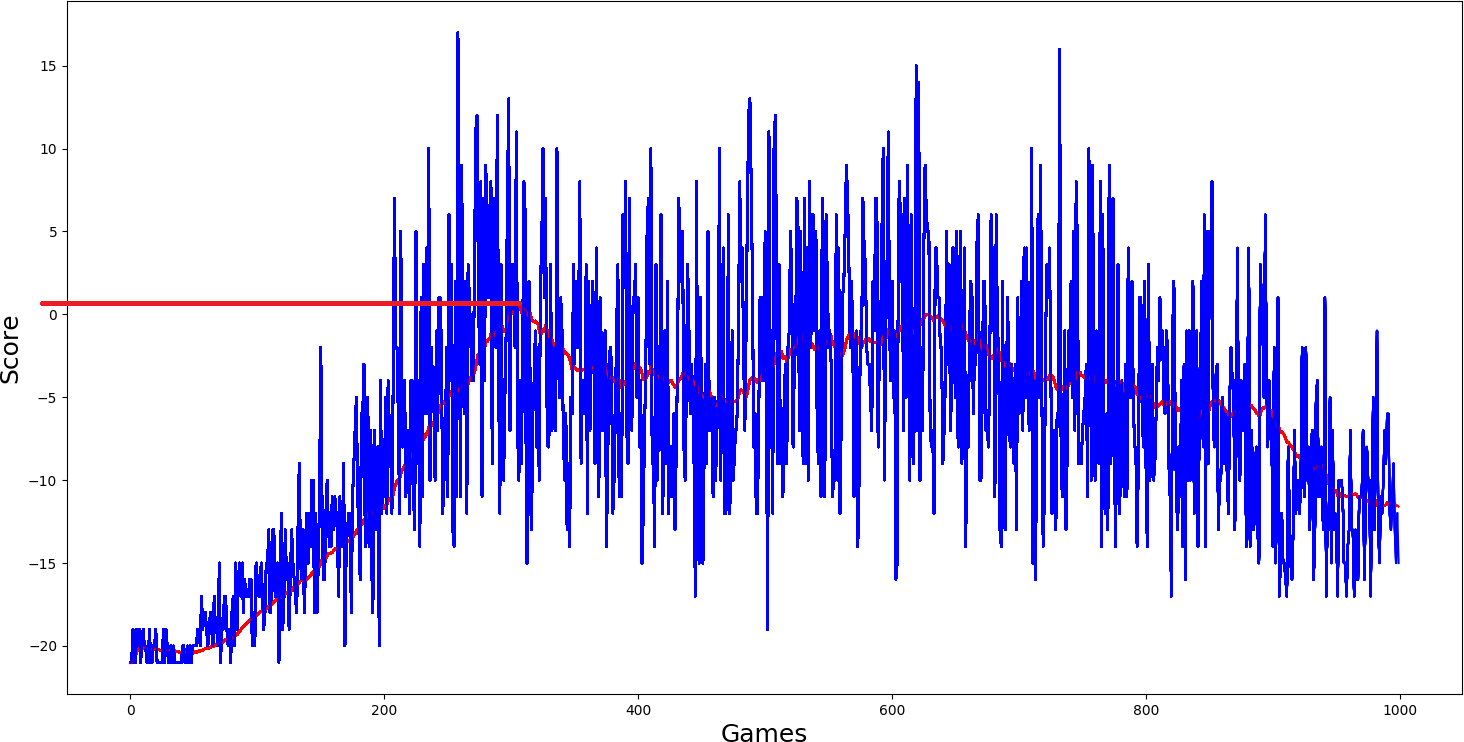
Here was my final hope self.USE_PER = True, because this performed best in our Cartpole game, it should be best here. But results were even worse:
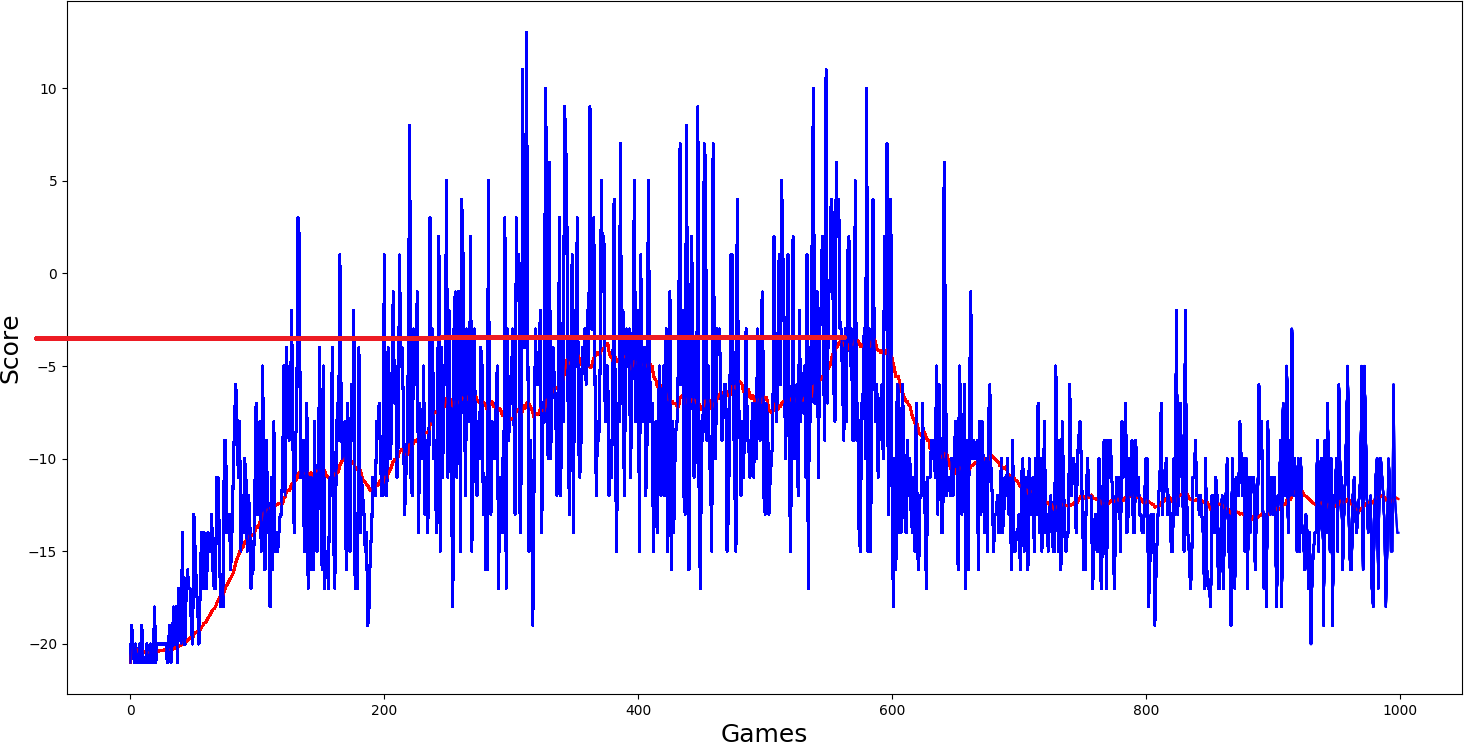
Conclusion:
From the above example results, I can say that when the environment for Q function is too complex to be learned, DQN will fail miserably. This is why this is my last DQN tutorial. Policy Gradients are generally believed to apply to a broader range of problems because they directly operate in the policy. So in the coming tutorial, I will cover Policy Gradient reinforcement learning.
