DQN PER with Convolutional Neural Networks

This tutorial will show you how to implement one of the most groundbreaking Reinforcement Learning algorithms - DQN with pixels. After the end of this tutorial, you will create an agent that successfully plays almost 'any' game using only pixel inputs.

We've used game-specific inputs in all my previous DQN tutorials (like cart position or pole angle). Now we will be more general and use something that all games have in common - pixels. To begin with, I would like to come back to our first DQN tutorial, where we wrote our first agent code to take actions randomly. Now we'll do the same thing, but instead of using specific environment inputs, we'll use pixels. This is our random action code from the first tutorial:

import gym
import random

env = gym.make("CartPole-v0")
env.reset()

def Random_games():
    for episode in range(10):
        env.reset()
        for t in range(500):
            env.render()
            action = env.action_space.sample()
            next_state, reward, done, info = env.step(action)
            print(t, next_state, reward, done, info, action)
            if done:
                break
                
Random_games()

This shortcode was playing random games for us, and now we'll need to build our own render, GetImage, reset and step functions to work with pixels.

Before we used env.render() function, when we wanted to see how our agent plays the game, in gym documentation, it's written that if we use env.render(mode='rgb_array') it will return us rendered frame image, this way, we'll get our image. Yes, it's sad that we'll need to render every frame of our game, it will be much slower than training without a render, but there is no other way to get game frames in a real situation. We could use different gym environment games to give us frames without rendering, but now we'll try a real-life example. So, here is the function to get rendered pixels:

img = env.render(mode='rgb_array') 

We'll see the following RGB image:

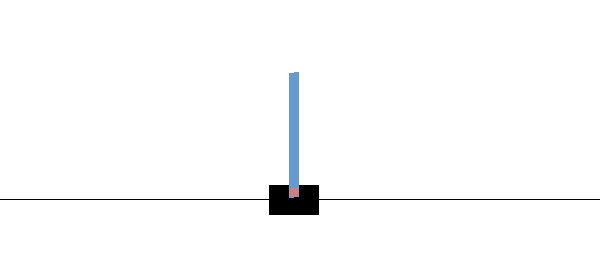
Cartpole gym environment outputs 600x400 RGB arrays (600x400x3). That’s way too many pixels with such a simple task, more than we need. We'll convert it to grayscale and downsize it with the following lines:

img_rgb = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
img_rgb_resized = cv2.resize(img_rgb, (240, 160), interpolation=cv2.INTER_CUBIC)

And we'll receive the following results:

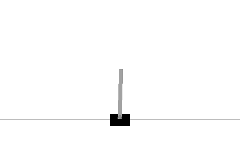
This will use fewer resources while training because of the image with 1 channel and smaller size, but to make everything simpler, we'll make it a full black Cartpole:

img_rgb_resized[img_rgb_resized < 255] = 0

So, for the final training result's we'll use the following images:

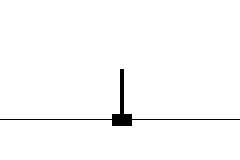
But do we have all the information to determine what’s really going on? No, we don’t have any information about the movements of the game objects, and I hope we all can agree that’s crucial in the world of games. So, how can we overcome this?

Let’s for each observation stack two consecutive frames:

Okay, now we can see the direction and the velocity of the pole. But do we know its acceleration? No. Let’s stack three frames then:

Now we can derive both the direction, velocity, and acceleration of the moving objects. Still, as not every game is rendered at the same pace, we’ll keep 4 frames - to be sure that we have all the necessary information:

Assuming that we will store four last frames for each step, our input shape will be 240x160x4. So now we'll do these steps? First, we'll define our 4 frame image memory: image_memory = np.zeros((4, 160, 240)). Every time before adding an image to our image_memory, we need to push our data by 1 frame, similar as deq() function work, by following way: image_memory = np.roll(image_memory, 1, axis = 0).

The last step is to add images to free space: image_memory[0,:,:] = img_rgb_resized.

So, this is how our complete code looks like for random steps:

import gym
import random
import numpy as np
import cv2

class DQN_CNN_Agent:
    def __init__(self, env_name):
        self.env_name = env_name       
        self.env = gym.make(env_name)
        self.ROWS = 160
        self.COLS = 240
        self.REM_STEP = 4

        self.EPISODES = 10

        self.image_memory = np.zeros((self.REM_STEP, self.ROWS, self.COLS))

    def imshow(self, image, rem_step=0):
        cv2.imshow(env_name+str(rem_step), image[rem_step,...])
        if cv2.waitKey(25) & 0xFF == ord("q"):
            cv2.destroyAllWindows()
            return

    def GetImage(self):
        img = self.env.render(mode='rgb_array')
  
        img_rgb = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
        img_rgb_resized = cv2.resize(img_rgb, (self.COLS, self.ROWS), interpolation=cv2.INTER_CUBIC)
        img_rgb_resized[img_rgb_resized < 255] = 0
        img_rgb_resized = img_rgb_resized / 255

        self.image_memory = np.roll(self.image_memory, 1, axis = 0)
        self.image_memory[0,:,:] = img_rgb_resized

        self.imshow(self.image_memory,0)
        
        return np.expand_dims(self.image_memory, axis=0)
    
    def reset(self):
        self.env.reset()
        for i in range(self.REM_STEP):
            state = self.GetImage()
        return state

    def step(self,action):
        next_state, reward, done, info = self.env.step(action)
        next_state = self.GetImage()
        return next_state, reward, done, info

    def run(self):
        # Each of this episode is its own game.
        for episode in range(self.EPISODES):
            self.reset()
            # this is each frame, up to 500...but we wont make it that far with random.
            for t in range(500):               
                # This will just create a sample action in any environment.
                # In this environment, the action can be 0 or 1, which is left or right
                action = self.env.action_space.sample()

                # this executes the environment with an action, 
                # and returns the observation of the environment, 
                # the reward, if the env is over, and other info.
                next_state, reward, done, info = self.step(action)
                
                # lets print everything in one line:
                #print(t, next_state, reward, done, info, action)
                if done:
                    break

if __name__ == "__main__":
    env_name = 'CartPole-v1'
    agent = DQN_CNN_Agent(env_name)
    agent.run()

You can test this random code by yourself, and it's pretty simple.

DQN with Convolutional Neural Network:

Before merging everything to one code, we must make one major improvement - implement Convolutional Neural Networks (CNN) to our current code. If you are not familiar with CNN, I have several tutorials about them; I recommend checking them out before moving forward. So, first, we'll implement few more functions for our CNN; we'll start with imports:

from keras.layers import Flatten, Conv2D, Activation

Bellow is already a modified agent model that we could use CNN. The input to the neural network will consist of 160 x 240 x 4 images. The first hidden layer convolves 64 filters of 5 x 5 with stride 3 with the input image and applies a ReLu activation. The second hidden layer convolves 64 filters of 4 x 4 with stride 2, followed by a ReLu activation. This is followed by a third convolutional layer that convolves 64 filters of 3 x 3 with stride 1 followed by a ReLu activation. The final hidden layer is fully connected to "Flatten" units. After these layers, goes all the same dense layers as before:

def OurModel(input_shape, action_space, dueling):
    X_input = Input(input_shape)
    X = X_input
    
    X = Conv2D(64, 5, strides=(3, 3),padding="valid", input_shape=input_shape, activation="relu", data_format="channels_first")(X)
    X = Conv2D(64, 4, strides=(2, 2),padding="valid", activation="relu", data_format="channels_first")(X)
    X = Conv2D(64, 3, strides=(1, 1),padding="valid", activation="relu", data_format="channels_first")(X)
    X = Flatten()(X)
    # 'Dense' is the basic form of a neural network layer
    # Input Layer of state size(4) and Hidden Layer with 512 nodes
    X = Dense(512, input_shape=input_shape, activation="relu", kernel_initializer='he_uniform')(X)

    # Hidden layer with 256 nodes
    X = Dense(256, activation="relu", kernel_initializer='he_uniform')(X)
    
    # Hidden layer with 64 nodes
    X = Dense(64, activation="relu", kernel_initializer='he_uniform')(X)

    if dueling:
        state_value = Dense(1, kernel_initializer='he_uniform')(X)
        state_value = Lambda(lambda s: K.expand_dims(s[:, 0], -1), output_shape=(action_space,))(state_value)

        action_advantage = Dense(action_space, kernel_initializer='he_uniform')(X)
        action_advantage = Lambda(lambda a: a[:, :] - K.mean(a[:, :], keepdims=True), output_shape=(action_space,))(action_advantage)

        X = Add()([state_value, action_advantage])
    else:
        # Output Layer with # of actions: 2 nodes (left, right)
        X = Dense(action_space, activation="linear", kernel_initializer='he_uniform')(X)

    model = Model(inputs = X_input, outputs = X, name='CartPole PER D3QN CNN model')
    model.compile(loss="mean_squared_error", optimizer=RMSprop(lr=0.00025, rho=0.95, epsilon=0.01), metrics=["accuracy"])

    model.summary()
    return model

Now it's time to merge the above random code functions (GetImage, reset, step) with our previous tutorials code. We'll remove the function from our previous tutorial, and we don't need this anymore because our input will be pixels. Now we'll use some newly defined variables:

self.ROWS = 160
self.COLS = 240
self.REM_STEP = 4

self.image_memory = np.zeros((self.REM_STEP, self.ROWS, self.COLS))
self.state_size = (self.REM_STEP, self.ROWS, self.COLS)

Here we defined our image size, which we'll give to our Neural Network; this is why we need to define the new self.state_size. Because of this change, we must make some changes in self.model and self.target_model to the following:

self.model = OurCnnModel(input_shape=self.state_size, action_space = self.action_size, dueling = self.dueling)
self.target_model = OurCnnModel(input_shape=self.state_size, action_space = self.action_size, dueling = self.dueling)

Because we changed inputs to our model, we must make changes in the replay function:

• We change state = np.zeros((self.batch_size, self.state_size)) to state = np.zeros((self.batch_size,) + self.state_size);
• We change next_state = np.zeros((self.batch_size, self.state_size)) to next_state = np.zeros((self.batch_size,) + self.state_size).

Also, as I told while merging the above code with previous tutorials code, in the main run function, we change:

• state = self.reset() to state = self.reset();
• self.env.step(action) to self.step(action).

Complete tutorial code on GitHub link:

# Tutorial by www.pylessons.com
# Tutorial written for - Tensorflow 1.15, Keras 2.2.4

import os
import random
import gym
import pylab
import numpy as np
from collections import deque
from keras.models import Model, load_model
from keras.layers import Input, Dense, Lambda, Add, Conv2D, Flatten
from keras.optimizers import Adam, RMSprop
from keras import backend as K
from PER import *
import cv2

def OurModel(input_shape, action_space, dueling):
    X_input = Input(input_shape)
    X = X_input
    
    X = Conv2D(64, 5, strides=(3, 3),padding="valid", input_shape=input_shape, activation="relu", data_format="channels_first")(X)
    X = Conv2D(64, 4, strides=(2, 2),padding="valid", activation="relu", data_format="channels_first")(X)
    X = Conv2D(64, 3, strides=(1, 1),padding="valid", activation="relu", data_format="channels_first")(X)
    X = Flatten()(X)
    # 'Dense' is the basic form of a neural network layer
    # Input Layer of state size(4) and Hidden Layer with 512 nodes
    X = Dense(512, activation="relu", kernel_initializer='he_uniform')(X)

    # Hidden layer with 256 nodes
    X = Dense(256, activation="relu", kernel_initializer='he_uniform')(X)
    
    # Hidden layer with 64 nodes
    X = Dense(64, activation="relu", kernel_initializer='he_uniform')(X)

    if dueling:
        state_value = Dense(1, kernel_initializer='he_uniform')(X)
        state_value = Lambda(lambda s: K.expand_dims(s[:, 0], -1), output_shape=(action_space,))(state_value)

        action_advantage = Dense(action_space, kernel_initializer='he_uniform')(X)
        action_advantage = Lambda(lambda a: a[:, :] - K.mean(a[:, :], keepdims=True), output_shape=(action_space,))(action_advantage)

        X = Add()([state_value, action_advantage])
    else:
        # Output Layer with # of actions: 2 nodes (left, right)
        X = Dense(action_space, activation="linear", kernel_initializer='he_uniform')(X)

    model = Model(inputs = X_input, outputs = X, name='CartPole PER D3QN CNN model')
    model.compile(loss="mean_squared_error", optimizer=RMSprop(lr=0.00025, rho=0.95, epsilon=0.01), metrics=["accuracy"])

    model.summary()
    return model

class DQNAgent:
    def __init__(self, env_name):
        self.env_name = env_name       
        self.env = gym.make(env_name)
        self.env.seed(0)  
        # by default, CartPole-v1 has max episode steps = 500
        # we can use this to experiment beyond 500
        self.env._max_episode_steps = 4000
        self.state_size = self.env.observation_space.shape[0]
        self.action_size = self.env.action_space.n
        self.EPISODES = 1000
        
        # Instantiate memory
        memory_size = 10000
        self.MEMORY = Memory(memory_size)
        self.memory = deque(maxlen=2000)

        self.gamma = 0.95    # discount rate
        
        # EXPLORATION HYPERPARAMETERS for epsilon and epsilon greedy strategy
        self.epsilon = 1.0  # exploration probability at start
        self.epsilon_min = 0.01  # minimum exploration probability 
        self.epsilon_decay = 0.0005  # exponential decay rate for exploration prob
        
        self.batch_size = 32

        # defining model parameters
        self.ddqn = True # use doudle deep q network
        self.Soft_Update = False # use soft parameter update
        self.dueling = True # use dealing netowrk
        self.epsilon_greedy = False # use epsilon greedy strategy
        self.USE_PER = True # use priority experienced replay
        
        self.TAU = 0.1 # target network soft update hyperparameter

        self.Save_Path = 'Models'
        if not os.path.exists(self.Save_Path): os.makedirs(self.Save_Path)
        self.scores, self.episodes, self.average = [], [], []

        self.Model_name = os.path.join(self.Save_Path, self.env_name+"_PER_D3QN_CNN.h5")

        self.ROWS = 160
        self.COLS = 240
        self.REM_STEP = 4

        self.image_memory = np.zeros((self.REM_STEP, self.ROWS, self.COLS))
        self.state_size = (self.REM_STEP, self.ROWS, self.COLS)
        
        # create main model and target model
        self.model = OurModel(input_shape=self.state_size, action_space = self.action_size, dueling = self.dueling)
        self.target_model = OurModel(input_shape=self.state_size, action_space = self.action_size, dueling = self.dueling)  

    # after some time interval update the target model to be same with model
    def update_target_model(self):
        if not self.Soft_Update and self.ddqn:
            self.target_model.set_weights(self.model.get_weights())
            return
        if self.Soft_Update and self.ddqn:
            q_model_theta = self.model.get_weights()
            target_model_theta = self.target_model.get_weights()
            counter = 0
            for q_weight, target_weight in zip(q_model_theta, target_model_theta):
                target_weight = target_weight * (1-self.TAU) + q_weight * self.TAU
                target_model_theta[counter] = target_weight
                counter += 1
            self.target_model.set_weights(target_model_theta)

    def remember(self, state, action, reward, next_state, done):
        experience = state, action, reward, next_state, done
        if self.USE_PER:
            self.MEMORY.store(experience)
        else:
            self.memory.append((experience))

    def act(self, state, decay_step):
        # EPSILON GREEDY STRATEGY
        if self.epsilon_greedy:
        # Here we'll use an improved version of our epsilon greedy strategy for Q-learning
            explore_probability = self.epsilon_min + (self.epsilon - self.epsilon_min) * np.exp(-self.epsilon_decay * decay_step)
        # OLD EPSILON STRATEGY
        else:
            if self.epsilon > self.epsilon_min:
                self.epsilon *= (1-self.epsilon_decay)
            explore_probability = self.epsilon
    
        if explore_probability > np.random.rand():
            # Make a random action (exploration)
            return random.randrange(self.action_size), explore_probability
        else:
            # Get action from Q-network (exploitation)
            # Estimate the Qs values state
            # Take the biggest Q value (= the best action)
            return np.argmax(self.model.predict(state)), explore_probability
                
    def replay(self):
        if self.USE_PER:
            # Sample minibatch from the PER memory
            tree_idx, minibatch  = self.MEMORY.sample(self.batch_size)
        else:
            # Randomly sample minibatch from the deque memory
            minibatch = random.sample(self.memory, min(len(self.memory), self.batch_size))

        state = np.zeros((self.batch_size,) + self.state_size)
        next_state = np.zeros((self.batch_size,) + self.state_size)
        action, reward, done = [], [], []

        # do this before prediction
        # for speedup, this could be done on the tensor level
        # but easier to understand using a loop       
        for i in range(len(minibatch)):
            state[i] = minibatch[i][0]
            action.append(minibatch[i][1])
            reward.append(minibatch[i][2])
            next_state[i] = minibatch[i][3]
            done.append(minibatch[i][4])

        # do batch prediction to save speed
        # predict Q-values for starting state using the main network
        target = self.model.predict(state)
        target_old = np.array(target)
        # predict best action in ending state using the main network
        target_next = self.model.predict(next_state)
        # predict Q-values for ending state using the target network
        target_val = self.target_model.predict(next_state)

        for i in range(len(minibatch)):
            # correction on the Q value for the action used
            if done[i]:
                target[i][action[i]] = reward[i]
            else:
                # the key point of Double DQN
                # selection of action is from model
                # update is from target model
                if self.ddqn: # Double - DQN
                    # current Q Network selects the action
                    # a'_max = argmax_a' Q(s', a')
                    a = np.argmax(target_next[i])
                    # target Q Network evaluates the action
                    # Q_max = Q_target(s', a'_max)
                    target[i][action[i]] = reward[i] + self.gamma * (target_val[i][a])
                else: # Standard - DQN
                    # DQN chooses the max Q value among next actions
                    # selection and evaluation of action is on the target Q Network
                    # Q_max = max_a' Q_target(s', a')
                    target[i][action[i]] = reward[i] + self.gamma * (np.amax(target_next[i]))

            if self.USE_PER:
                absolute_errors = np.abs(target_old[i]-target[i])
                # Update priority
                self.MEMORY.batch_update(tree_idx, absolute_errors)
                
        # Train the Neural Network with batches
        self.model.fit(state, target, batch_size=self.batch_size, verbose=0)

    def load(self, name):
        self.model = load_model(name)

    def save(self, name):
        self.model.save(name)

    pylab.figure(figsize=(18, 9))
    def PlotModel(self, score, episode):
        self.scores.append(score)
        self.episodes.append(episode)
        self.average.append(sum(self.scores[-50:]) / len(self.scores[-50:]))
        pylab.plot(self.episodes, self.average, 'r')
        pylab.plot(self.episodes, self.scores, 'b')
        pylab.ylabel('Score', fontsize=18)
        pylab.xlabel('Steps', fontsize=18)
        dqn = 'DQN_'
        softupdate = ''
        dueling = ''
        greedy = ''
        PER = ''
        if self.ddqn: dqn = 'DDQN_'
        if self.Soft_Update: softupdate = '_soft'
        if self.dueling: dueling = '_Dueling'
        if self.epsilon_greedy: greedy = '_Greedy'
        if self.USE_PER: PER = '_PER'
        try:
            pylab.savefig(dqn+self.env_name+softupdate+dueling+greedy+PER+"_CNN.png")
        except OSError:
            pass

        return str(self.average[-1])[:5]

    def imshow(self, image, rem_step=0):
        cv2.imshow("cartpole"+str(rem_step), image[rem_step,...])
        if cv2.waitKey(25) & 0xFF == ord("q"):
            cv2.destroyAllWindows()
            return

    def GetImage(self):
        img = self.env.render(mode='rgb_array')
        
        img_rgb = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
        img_rgb_resized = cv2.resize(img_rgb, (self.COLS, self.ROWS), interpolation=cv2.INTER_CUBIC)
        img_rgb_resized[img_rgb_resized < 255] = 0
        img_rgb_resized = img_rgb_resized / 255

        self.image_memory = np.roll(self.image_memory, 1, axis = 0)
        self.image_memory[0,:,:] = img_rgb_resized

        #self.imshow(self.image_memory,0)
        
        return np.expand_dims(self.image_memory, axis=0)

    def reset(self):
        self.env.reset()
        for i in range(self.REM_STEP):
            state = self.GetImage()
        return state

    def step(self,action):
        next_state, reward, done, info = self.env.step(action)
        next_state = self.GetImage()
        return next_state, reward, done, info
    
    def run(self):
        decay_step = 0
        for e in range(self.EPISODES):
            state = self.reset()
            done = False
            i = 0
            while not done:
                decay_step += 1
                action, explore_probability = self.act(state, decay_step)
                next_state, reward, done, _ = self.step(action)
                if not done or i == self.env._max_episode_steps-1:
                    reward = reward
                else:
                    reward = -100
                self.remember(state, action, reward, next_state, done)
                state = next_state
                i += 1
                if done:
                    # every REM_STEP update target model
                    if e % self.REM_STEP == 0:
                        self.update_target_model()
                    
                    # every episode, plot the result
                    average = self.PlotModel(i, e)
                    
                    print("episode: {}/{}, score: {}, e: {:.2}, average: {}".format(e, self.EPISODES, i, explore_probability, average))
                    if i == self.env._max_episode_steps:
                        print("Saving trained model to", self.Model_name)
                        #self.save(self.Model_name)
                        break
                self.replay()

    def test(self):
        self.load(self.Model_name)
        for e in range(self.EPISODES):
            state = self.reset()
            done = False
            i = 0
            while not done:
                action = np.argmax(self.model.predict(state))
                next_state, reward, done, _ = env.step(action)
                i += 1
                if done:
                    print("episode: {}/{}, score: {}".format(e, self.EPISODES, i))
                    break

if __name__ == "__main__":
    env_name = 'CartPole-v1'
    agent = DQNAgent(env_name)
    agent.run()
    #agent.test()

DQN CNN agent performance

I think you are interested in how our new agent performed simply with pixel inputs. I will tell you, not that well as I wanted/expected. But at least we can see that it's working, there is a lot where to improve.

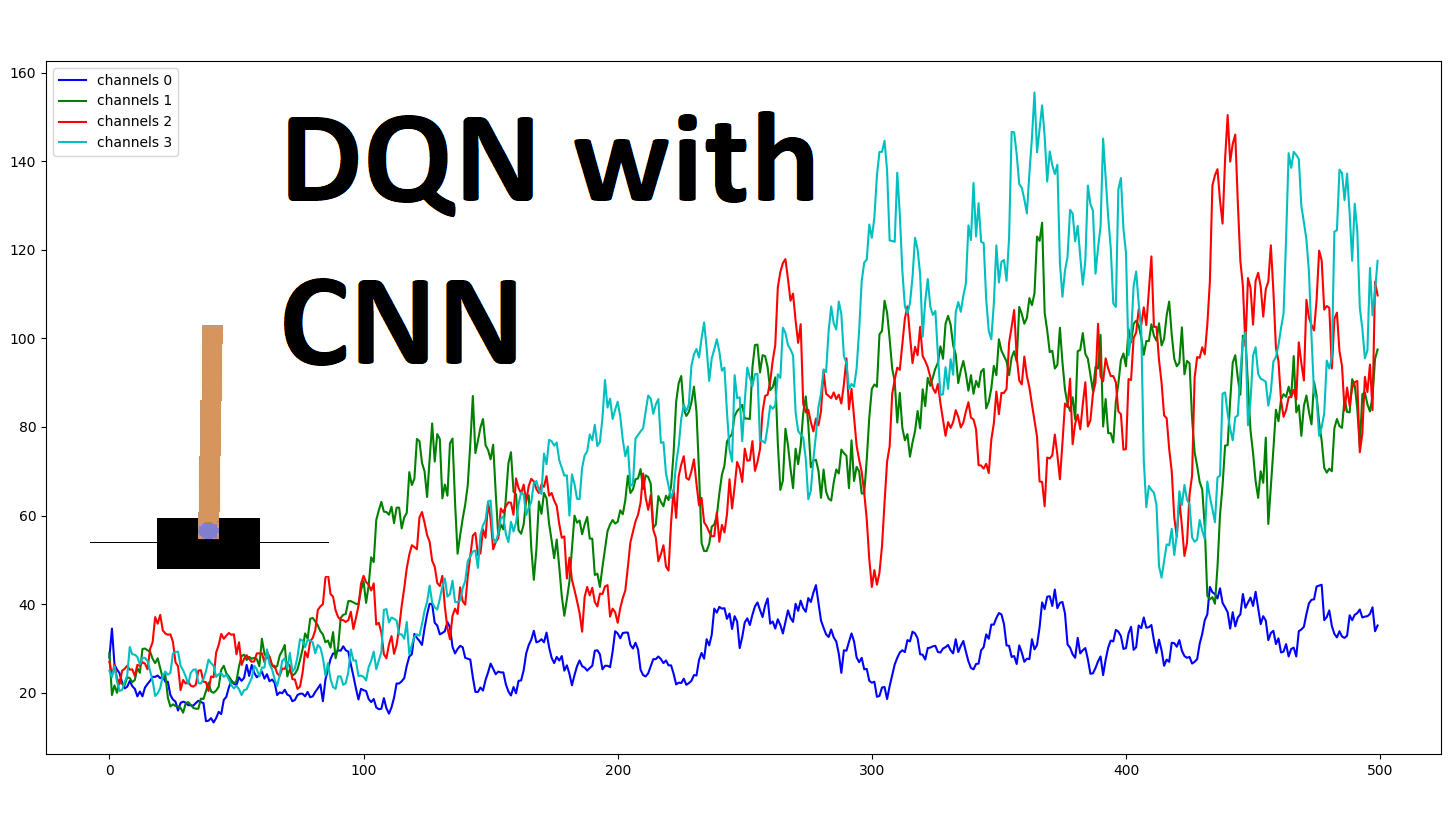
So, the same as before, I trained an agent for 500 episodes to save my time. But as I told you, that this time we'd be keeping current and three history images; I did training tests for 1, 2, 3, and 4 history images, results:

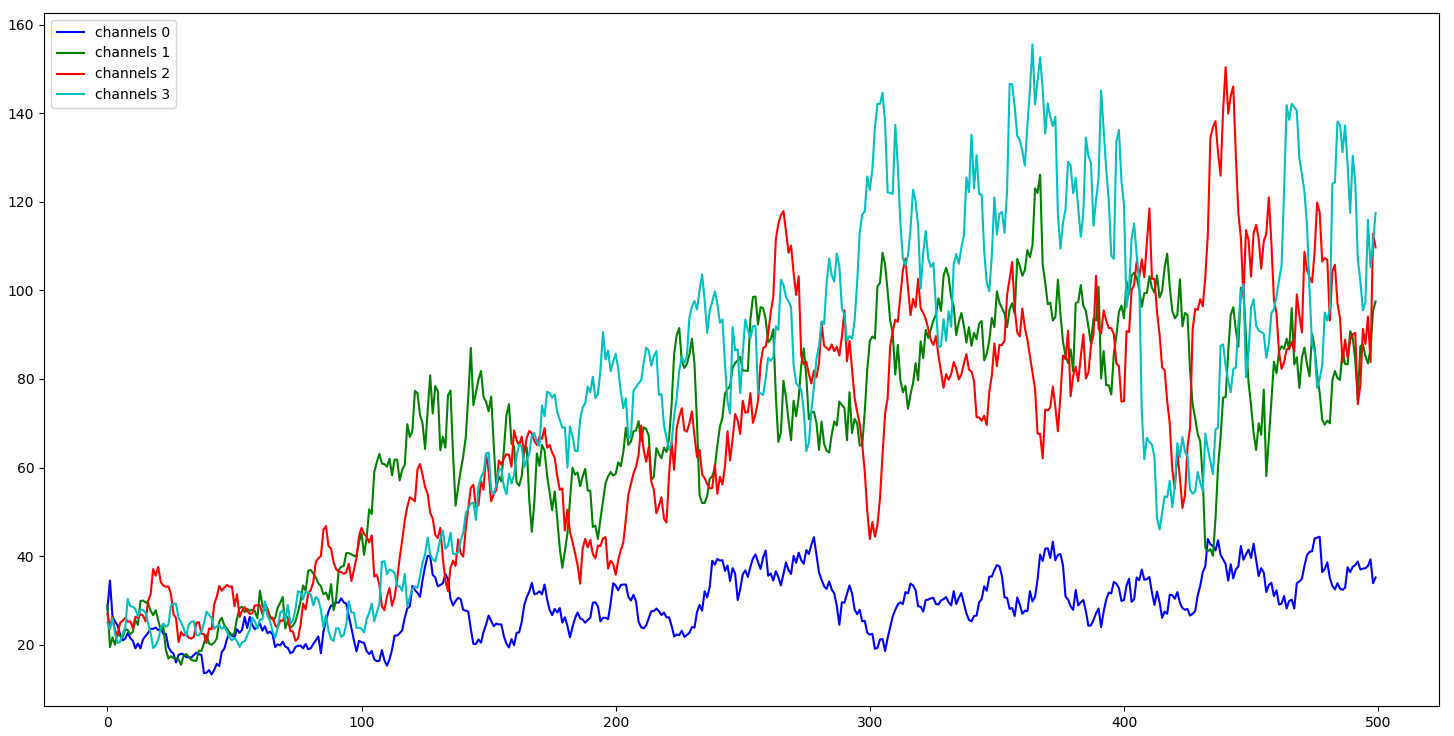
From the above chart, we can see that our agent, just with one input (channels 0), performed the worsts; even our random agent could perform similarly. Then we can see that agents who have more channels than one performs better, and we can assume that the more channels our agent see, the better it performed. But there is one minus - more channels it has - more resources are needed for training. So, I tried to train four channels agent for longer, and I trained it for around 3600 steps:

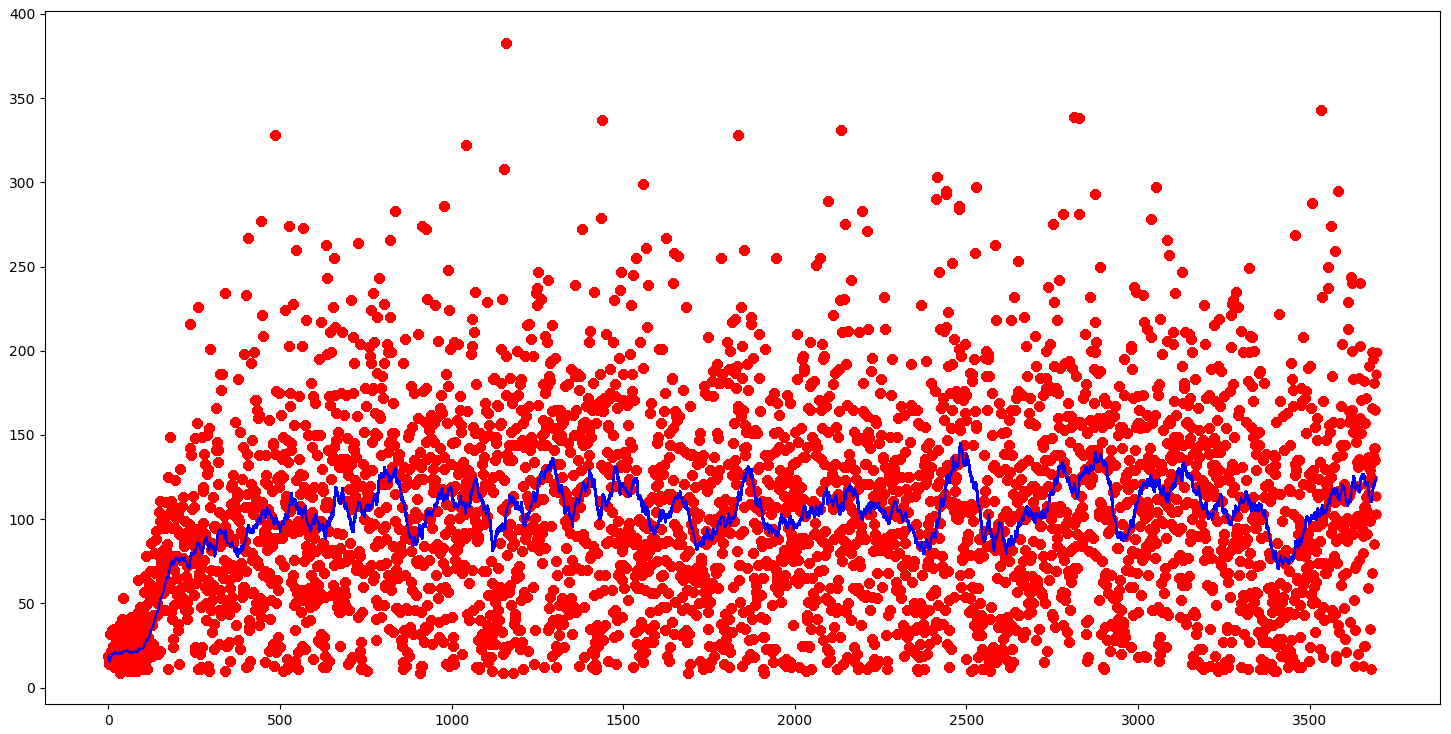
The red dots in the graph are the actual episode score, and the blue line is the 50 games moving average score. Our agent reached the best performance in around 1000 training steps, which was not improving anymore. Our average game score was about 100; it's much worse than using four parameters as input than pixels, but it's impossible to get the best input parameters; they always have some noise or error.