In the previous tutorial, I said that we'd try to implement the Prioritized Experience Replay (PER) method in the next tutorial. Still, before doing that, I decided that we should cover the Epsilon Greedy fix/prepare the source code for PER method. So this will be quite a short tutorial.
The epsilon-greedy algorithm is straightforward and occurs in several areas of machine learning. One everyday use of epsilon-greedy is in the so-called multi-armed bandit problem.
Let's take an example. Suppose we are standing in front of three slot machines. Each of these machines payout according to a different probability distribution that is unknown to us. And suppose we can play a total of 100 times.
We have two goals. One of them is to win as much money as possible. The second goal is to use some coins to try and determine which machine pays out the best. The terms "exploit" and "explore" are used to indicate that we will use some coins to explore to find the best machine, and in the end, we want to use most of the coins on the best machine to exploit our knowledge.
Epsilon-greedy is almost too simple. As we play the machines, we keep track of the average payout of each machine. Then, we choose a machine with the highest average payout rate that probability we can calculate with the following formula: probability = (1 – epsilon) + (epsilon / k)Where epsilon is a small value like 0.10. In the end, we select machines that don't have the highest current payout average with probability = epsilon / k.
It's much easier to understand with a concrete example. Suppose, after our first 12 pulls, we played machine #1 four times and won 1 dollar two times and 0 dollars two times. The average win rate for machine #1 is 2/4 = 0.50 dollars.
And suppose we've played machine #2 five times and won 1 dollar three times and 0 dollars two times. Now, the average payout for machine #2 is 3/5 = 0.60 dollars.
And suppose we've played machine #3 three times and won 1 dollar one time and 0 dollars two times. Then the average payout for machine #3 is 1/3 = 0.33 dollars.
Now we have to select a machine to play on. We generate a random number p, between 0.0 and 1.0. Suppose we have set epsilon = 0.10. If p > 0.10 (which will be 90% of the time), we select machine #2 because it has the current highest average payout. But if p < 0.10 (which will be only 10% of the time), we randomly select a machine, so each machine will have a 33.3% probability of being selected. Note that machine #2 might get picked anyway; this is because we choose randomly from all our machines.
Over time, the best machine will be played more and more often as it pays off more often. In short, an epsilon-greedy means choosing the best ("greedy") option at the moment, but sometimes choosing a random option that is unlikely (epsilon).
There are many other algorithms to help solve the problem of a multi-armed bandit. However, epsilon greed is incredibly simple and often works the same, or even better, than more sophisticated algorithms such as UCB ("upper confidence limit") variants.
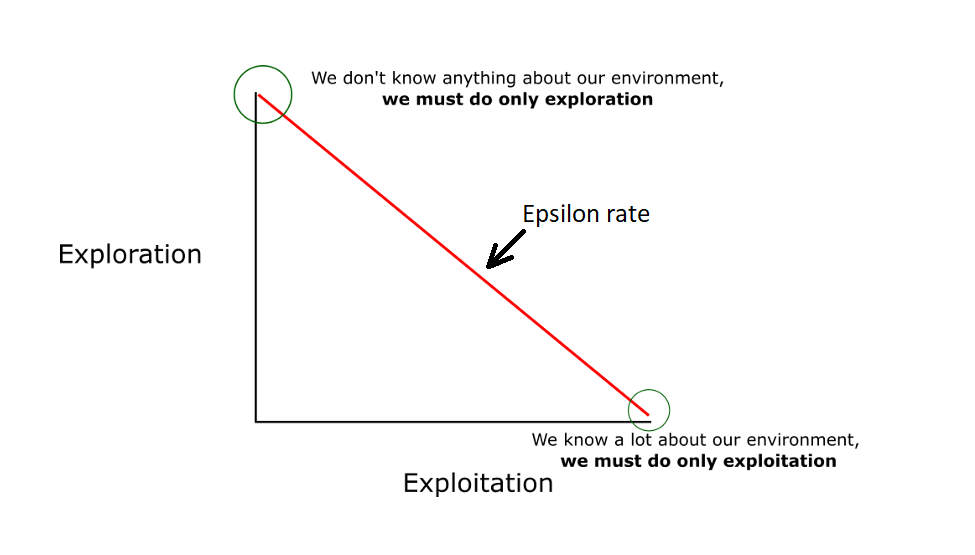
The idea is that we will initially use the epsilon greedy strategy:
- We specify an exploration rate - epsilon, which we initially set to 1. This is the frequency of the steps we will do randomly. In the beginning, this rate should be the highest value because we know nothing about the importance of the Q table. This means that we have to do a lot of research by randomly choosing our actions;
- We generate a random number. If this number is larger than epsilon, then we will do the "exploitation" (meaning that we are sure we are selecting the best action at each step). Otherwise, we will do research;
- The idea is that we need to have a big epsilon at the beginning of Q function training. Then gradually reduce it as the agent has more confidence in the Q values.
So, what we changed in the code? It almost didn't change. We inserted self.epsilon_greedy = True # use epsilon greedy strategy Boolean option if we want to use this method or not. Exploration hyper-parameters for epsilon and epsilon greedy strategy will be quite the same:
self.epsilon = 1.0 # exploration probability at start
self.epsilon_min = 0.01 # minimum exploration probability
self.epsilon_decay = 0.0005 # exponential decay rate for exploration probFrom our previous tutorial, we have the following "remember" function:
def remember(self, state, action, reward, next_state, done):
self.memory.append((state, action, reward, next_state, done))
if len(self.memory) > self.train_start:
if self.epsilon > self.epsilon_min:
self.epsilon *= self.epsilon_decayWe change it to the following:
def remember(self, state, action, reward, next_state, done):
experience = state, action, reward, next_state, done
self.memory.append((experience))Before, we were checking if our memory list is equal to self.train_start. We'll do training from our first episode of the game, and we won't fill memory with samples. So, we are removing all lines, and we'll implement the epsilon greedy function in different places.
Until now, we were doing the following "act" function:
def act(self, state):
if np.random.random() <= self.epsilon:
return random.randrange(self.action_size)
else:
return np.argmax(self.model.predict(state))But now, we'll implement another epsilon greedy function, where we could change our used epsilon method with Boolean. We'll use an improved version of our epsilon greedy strategy for Q-learning, where we gradually reduce the epsilon as the agent becomes more confident in estimating the Q-values. The function is almost the same, and we inserted explore_probability calculation into the epsilon greedy strategy:
def act(self, state, decay_step):
# EPSILON GREEDY STRATEGY
if self.epsilon_greedy:
# Here we'll use an improved version of our epsilon greedy strategy for Q-learning
explore_probability = self.epsilon_min + (self.epsilon - self.epsilon_min) * np.exp(-self.epsilon_decay * decay_step)
# OLD EPSILON STRATEGY
else:
if self.epsilon > self.epsilon_min:
self.epsilon *= (1-self.epsilon_decay)
explore_probability = self.epsilon
if explore_probability > np.random.rand():
# Make a random action (exploration)
return random.randrange(self.action_size), explore_probability
else:
# Get action from Q-network (exploitation)
# Estimate the Qs values state
# Take the biggest Q value (= the best action)
return np.argmax(self.model.predict(state)), explore_probabilityIn all code, I am removing the following lines to start training agent from the first steps:
if len(self.memory) < self.train_start:
returnAnd finally, we are modifying our def run(self): function:
- Inserting
decay_step = 0variable anddecay_step += 1function in a while loop; - Instead of old
action = self.act(state)function we call it in the following way:action, explore_probability = self.act(state, decay_step); - We change our logging print line, where before we were printing
self.epsilon, now we'll printexplore_probabilityin this place.
So, there weren't a lot of changes, but we still need to do them; here is the complete tutorial code on the GitHub link:
# Tutorial by www.pylessons.com
# Tutorial written for - Tensorflow 1.15, Keras 2.2.4
import os
import random
import gym
import pylab
import numpy as np
from collections import deque
from keras.models import Model, load_model
from keras.layers import Input, Dense, Lambda, Add
from keras.optimizers import Adam, RMSprop
from keras import backend as K
def OurModel(input_shape, action_space, dueling):
X_input = Input(input_shape)
X = X_input
# 'Dense' is the basic form of a neural network layer
# Input Layer of state size(4) and Hidden Layer with 512 nodes
X = Dense(512, input_shape=input_shape, activation="relu", kernel_initializer='he_uniform')(X)
# Hidden layer with 256 nodes
X = Dense(256, activation="relu", kernel_initializer='he_uniform')(X)
# Hidden layer with 64 nodes
X = Dense(64, activation="relu", kernel_initializer='he_uniform')(X)
if dueling:
state_value = Dense(1, kernel_initializer='he_uniform')(X)
state_value = Lambda(lambda s: K.expand_dims(s[:, 0], -1), output_shape=(action_space,))(state_value)
action_advantage = Dense(action_space, kernel_initializer='he_uniform')(X)
action_advantage = Lambda(lambda a: a[:, :] - K.mean(a[:, :], keepdims=True), output_shape=(action_space,))(action_advantage)
X = Add()([state_value, action_advantage])
else:
# Output Layer with # of actions: 2 nodes (left, right)
X = Dense(action_space, activation="linear", kernel_initializer='he_uniform')(X)
model = Model(inputs = X_input, outputs = X, name='CartPole Dueling DDQN model')
model.compile(loss="mean_squared_error", optimizer=RMSprop(lr=0.00025, rho=0.95, epsilon=0.01), metrics=["accuracy"])
model.summary()
return model
class DQNAgent:
def __init__(self, env_name):
self.env_name = env_name
self.env = gym.make(env_name)
self.env.seed(0)
# by default, CartPole-v1 has max episode steps = 500
self.env._max_episode_steps = 4000
self.state_size = self.env.observation_space.shape[0]
self.action_size = self.env.action_space.n
self.EPISODES = 1000
self.memory = deque(maxlen=2000)
self.gamma = 0.95 # discount rate
# EXPLORATION HYPERPARAMETERS for epsilon and epsilon greedy strategy
self.epsilon = 1.0 # exploration probability at start
self.epsilon_min = 0.01 # minimum exploration probability
self.epsilon_decay = 0.0005 # exponential decay rate for exploration prob
self.batch_size = 32
# defining model parameters
self.ddqn = True # use double deep q network
self.Soft_Update = False # use soft parameter update
self.dueling = True # use dealing network
self.epsilon_greedy = True # use epsilon greedy strategy
self.TAU = 0.1 # target network soft update hyperparameter
self.Save_Path = 'Models'
if not os.path.exists(self.Save_Path): os.makedirs(self.Save_Path)
self.scores, self.episodes, self.average = [], [], []
self.Model_name = os.path.join(self.Save_Path, self.env_name+"_e_greedy.h5")
# create main model and target model
self.model = OurModel(input_shape=(self.state_size,), action_space = self.action_size, dueling = self.dueling)
self.target_model = OurModel(input_shape=(self.state_size,), action_space = self.action_size, dueling = self.dueling)
# after some time interval update the target model to be same with model
def update_target_model(self):
if not self.Soft_Update and self.ddqn:
self.target_model.set_weights(self.model.get_weights())
return
if self.Soft_Update and self.ddqn:
q_model_theta = self.model.get_weights()
target_model_theta = self.target_model.get_weights()
counter = 0
for q_weight, target_weight in zip(q_model_theta, target_model_theta):
target_weight = target_weight * (1-self.TAU) + q_weight * self.TAU
target_model_theta[counter] = target_weight
counter += 1
self.target_model.set_weights(target_model_theta)
def remember(self, state, action, reward, next_state, done):
experience = state, action, reward, next_state, done
self.memory.append((experience))
def act(self, state, decay_step):
# EPSILON GREEDY STRATEGY
if self.epsilon_greedy:
# Here we'll use an improved version of our epsilon greedy strategy for Q-learning
explore_probability = self.epsilon_min + (self.epsilon - self.epsilon_min) * np.exp(-self.epsilon_decay * decay_step)
# OLD EPSILON STRATEGY
else:
if self.epsilon > self.epsilon_min:
self.epsilon *= (1-self.epsilon_decay)
explore_probability = self.epsilon
if explore_probability > np.random.rand():
# Make a random action (exploration)
return random.randrange(self.action_size), explore_probability
else:
# Get action from Q-network (exploitation)
# Estimate the Qs values state
# Take the biggest Q value (= the best action)
return np.argmax(self.model.predict(state)), explore_probability
def replay(self):
if len(self.memory) < self.batch_size:
return
# Randomly sample minibatch from the memory
minibatch = random.sample(self.memory, self.batch_size)
state = np.zeros((self.batch_size, self.state_size))
next_state = np.zeros((self.batch_size, self.state_size))
action, reward, done = [], [], []
# do this before prediction
# for speedup, this could be done on the tensor level
# but easier to understand using a loop
for i in range(self.batch_size):
state[i] = minibatch[i][0]
action.append(minibatch[i][1])
reward.append(minibatch[i][2])
next_state[i] = minibatch[i][3]
done.append(minibatch[i][4])
# do batch prediction to save speed
# predict Q-values for starting state using the main network
target = self.model.predict(state)
# predict best action in ending state using the main network
target_next = self.model.predict(next_state)
# predict Q-values for ending state using the target network
target_val = self.target_model.predict(next_state)
for i in range(len(minibatch)):
# correction on the Q value for the action used
if done[i]:
target[i][action[i]] = reward[i]
else:
if self.ddqn: # Double - DQN
# current Q Network selects the action
# a'_max = argmax_a' Q(s', a')
a = np.argmax(target_next[i])
# target Q Network evaluates the action
# Q_max = Q_target(s', a'_max)
target[i][action[i]] = reward[i] + self.gamma * (target_val[i][a])
else: # Standard - DQN
# DQN chooses the max Q value among next actions
# selection and evaluation of action is on the target Q Network
# Q_max = max_a' Q_target(s', a')
target[i][action[i]] = reward[i] + self.gamma * (np.amax(target_next[i]))
# Train the Neural Network with batches
self.model.fit(state, target, batch_size=self.batch_size, verbose=0)
def load(self, name):
self.model = load_model(name)
def save(self, name):
self.model.save(name)
pylab.figure(figsize=(18, 9))
def PlotModel(self, score, episode):
self.scores.append(score)
self.episodes.append(episode)
self.average.append(sum(self.scores[-50:]) / len(self.scores[-50:]))
pylab.plot(self.episodes, self.average, 'r')
pylab.plot(self.episodes, self.scores, 'b')
pylab.ylabel('Score', fontsize=18)
pylab.xlabel('Steps', fontsize=18)
dqn = 'DQN_'
softupdate = ''
dueling = ''
greedy = ''
if self.ddqn: dqn = 'DDQN_'
if self.Soft_Update: softupdate = '_soft'
if self.dueling: dueling = '_Dueling'
if self.epsilon_greedy: greedy = '_Greedy'
try:
pylab.savefig(dqn+self.env_name+softupdate+dueling+greedy+".png")
except OSError:
pass
return str(self.average[-1])[:5]
def run(self):
decay_step = 0
for e in range(self.EPISODES):
state = self.env.reset()
state = np.reshape(state, [1, self.state_size])
done = False
i = 0
while not done:
#self.env.render()
decay_step += 1
action, explore_probability = self.act(state, decay_step)
next_state, reward, done, _ = self.env.step(action)
next_state = np.reshape(next_state, [1, self.state_size])
if not done or i == self.env._max_episode_steps-1:
reward = reward
else:
reward = -100
self.remember(state, action, reward, next_state, done)
state = next_state
i += 1
if done:
# every step update target model
self.update_target_model()
# every episode, plot the result
average = self.PlotModel(i, e)
print("episode: {}/{}, score: {}, e: {:.2}, average: {}".format(e, self.EPISODES, i, explore_probability, average))
if i == self.env._max_episode_steps:
print("Saving trained model to", self.Model_name)
self.save(self.Model_name)
break
self.replay()
def test(self):
self.load(self.Model_name)
for e in range(self.EPISODES):
state = self.env.reset()
state = np.reshape(state, [1, self.state_size])
done = False
i = 0
while not done:
self.env.render()
action = np.argmax(self.model.predict(state))
next_state, reward, done, _ = self.env.step(action)
state = np.reshape(next_state, [1, self.state_size])
i += 1
if done:
print("episode: {}/{}, score: {}".format(e, self.EPISODES, i))
break
if __name__ == "__main__":
env_name = 'CartPole-v1'
agent = DQNAgent(env_name)
agent.run()
#agent.test()Here are the results of the epsilon greedy strategy playing it for 1000 steps:
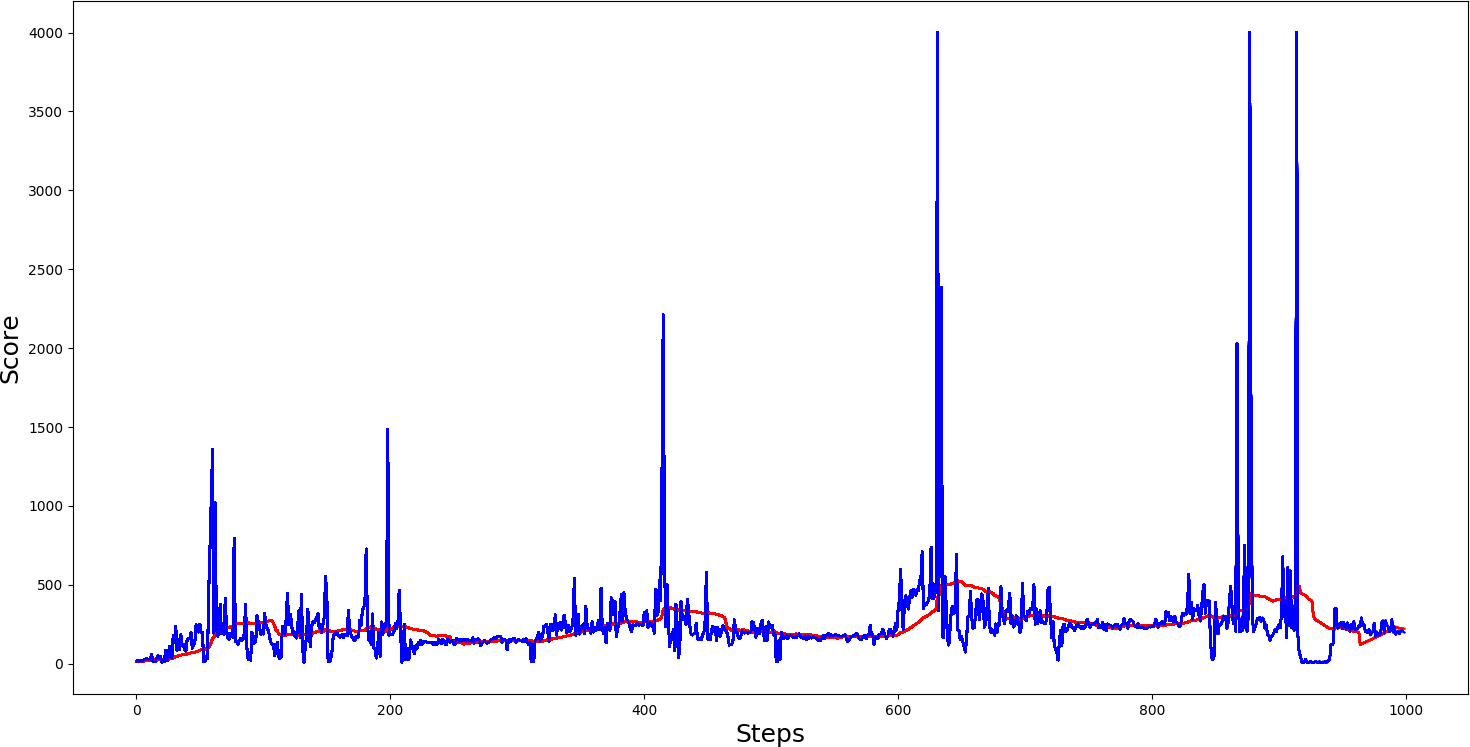
Conclusion:
I won't compare how our agent performs with epsilon greedy and without greedy because before, we used a very similar strategy to reduce epsilon, there won't be a significant difference. But for your interest, above is the results of how epsilon greedy performs.
In this short tutorial, we prepared our code for the coming tutorial. We'll integrate the Priority Experience Replay method to our agent; with this method, our agent should improve significantly, so keep watching!